مضارب اعداد و محاسبه کوچکترین مضرب مشترک (ک م م) | یک روش بدست آوردن ک م م، تجزیه عددها و محاسبه حاصلضرب عامل های مشترک با توان بیشتر در عامل های غیر مشترک آن عددها است
فهرست محتوا
مضرب های یک عدد
مضرب های یک عدد را می توانیم به صورت جمع های از آن عدد و یا با ضرب آن عدد در اعداد طبیعی بدست آورد.
به طور مثال می خواهیم مضارب عدد 3 را بدست بیاوریم
در سطر اول عدد 3 را نوشته و در هر سطر جدید حاصل جمع، مقدار سطر قبلی را با عدد 3 می نویسیم
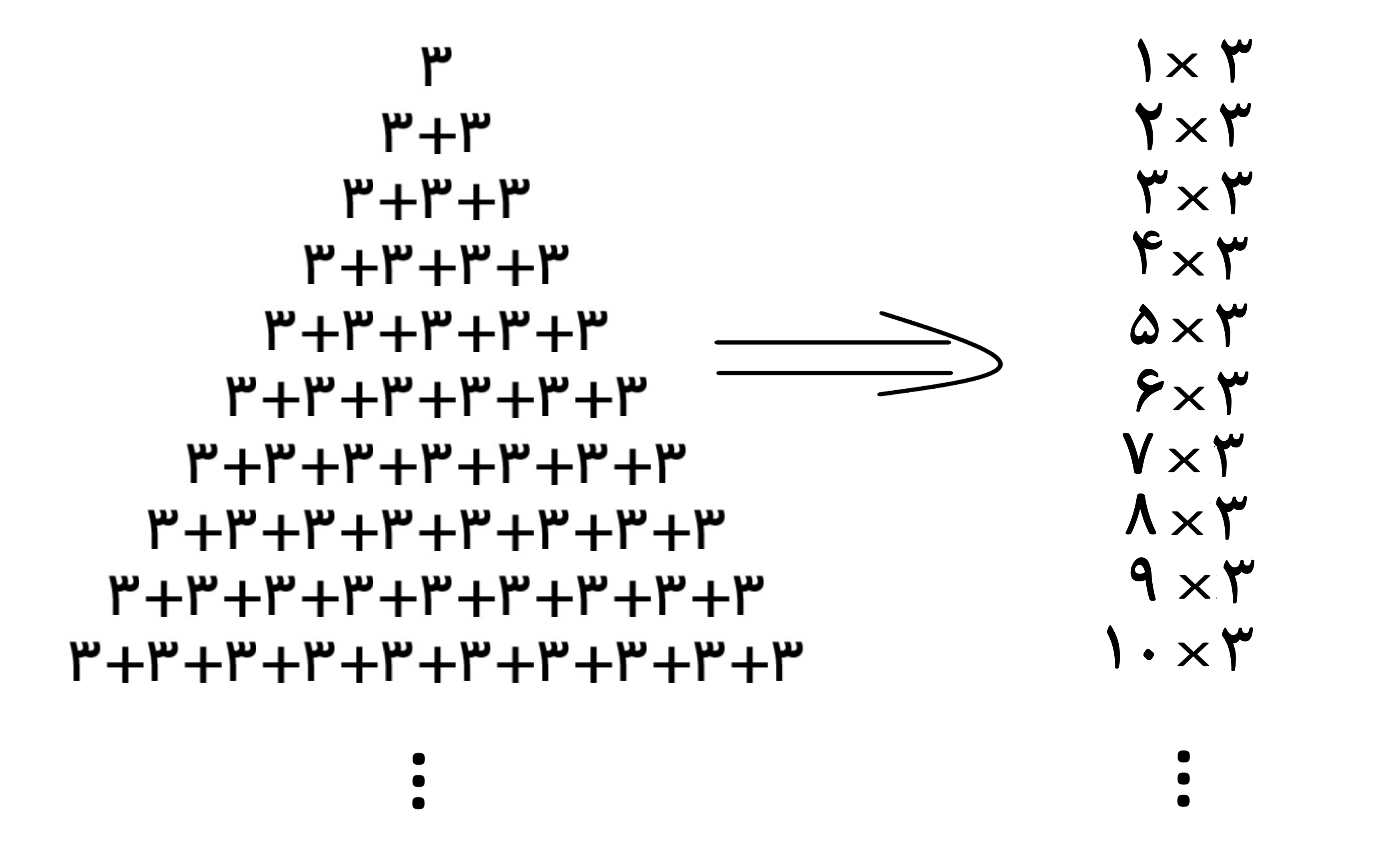
نتیجه را می توان به صورت حاصل ضرب تعداد دفعات تکرار عدد 3 نوشت.
روش دیگر؛ از عدد 3 شروع می کنیم و هر بار برای بدست آوردن عدد جدیدی که مضرب 3 هست، 3 تا به عدد قبل اضافه می کنیم
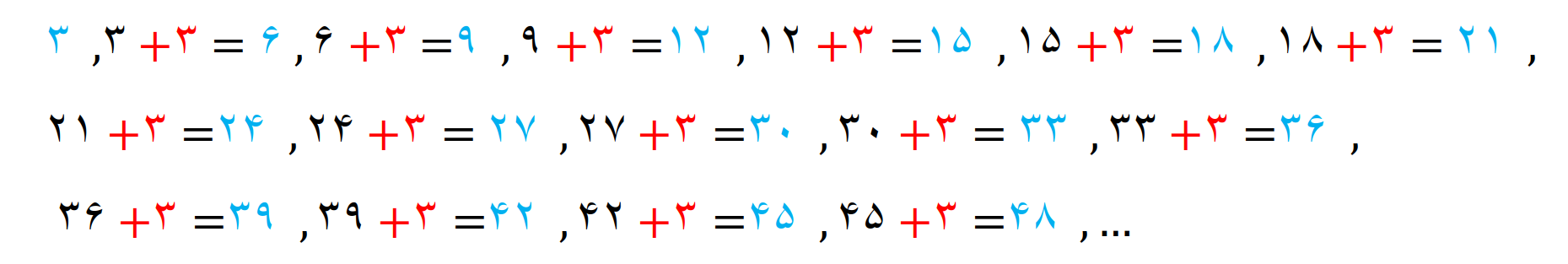
عددهای که به رنگ آبی هستند مضرب های 3 می باشند که از این راه بدست آوردیم
راحت ترین روش برای بدست آوردن مضرب های 3 این است که، عدد 3 را در اعداد طبیعی ضرب کنیم
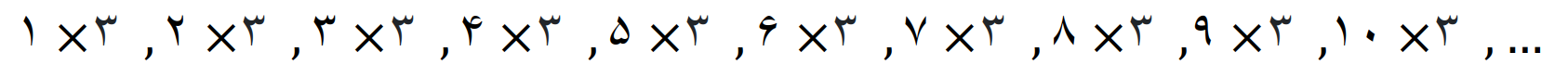
حاصل ضرب های بالا، را می نویسیم
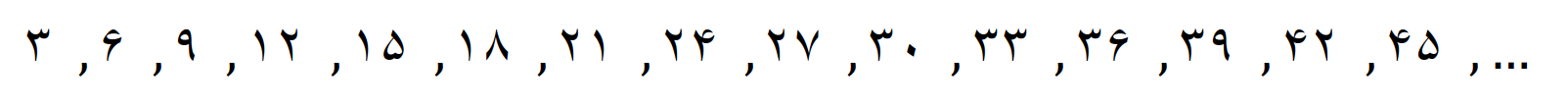
این عددها مضرب 3 هستند
مثال 1
مضرب های اعداد 2، 3، 4، … و 11 را بنویسید
جواب: برای بدست آوردن مضرب های این اعداد کافی است هر کدام از آن ها را در اعداد طبیعی ضرب کنیم
مضرب های 2
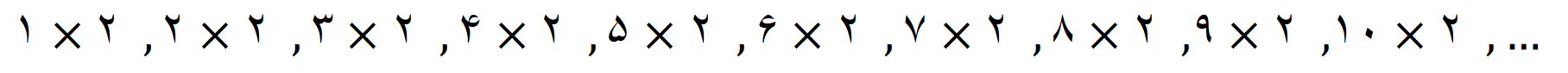
حاصل این ضرب ها را می نویسیم
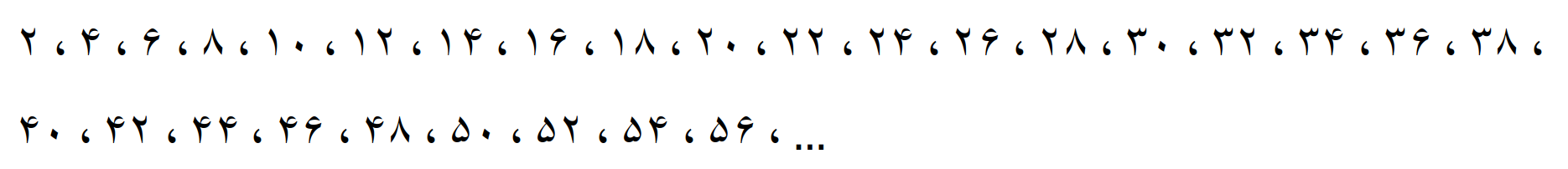
این عددها مضرب 2 هستند.
مضرب های 3
عدد 3 را در اعداد طبیعی ضرب می کنیم
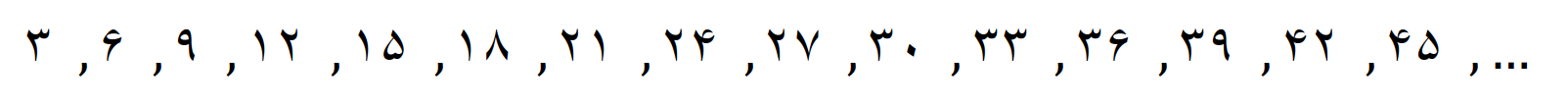
این عددها مضرب 3 هستند.
مضرب های 4
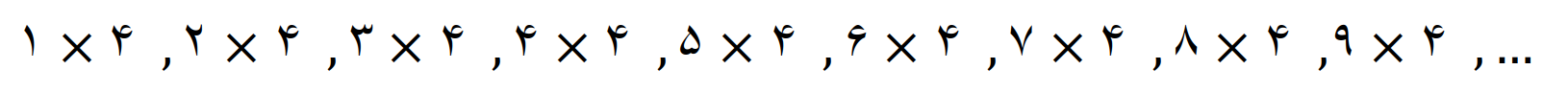
حاصل این ضرب ها را می نویسیم
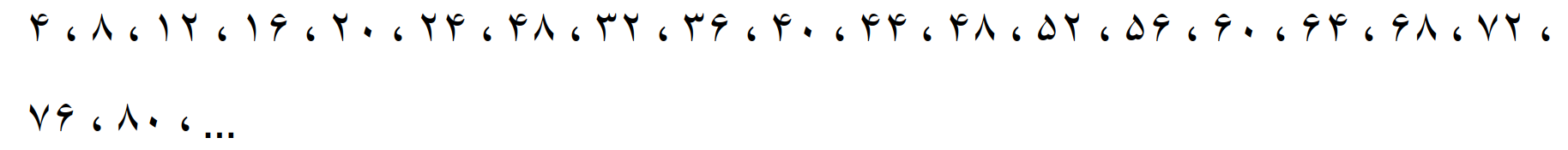
این عددها مضرب 4 هستند.
مضرب های 5
عدد 5 را در اعداد طبیعی ضرب می کنیم حاصل مضرب های 5 خواهد بود
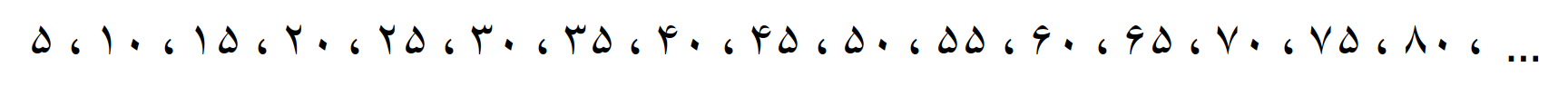
مضرب های 6
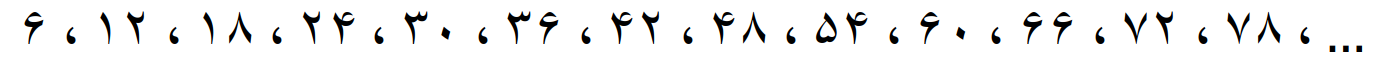
مضرب های 7
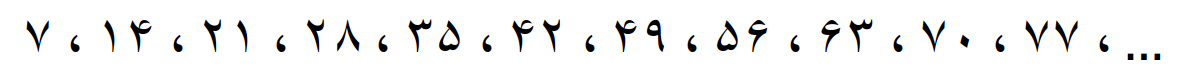
مضرب های 8
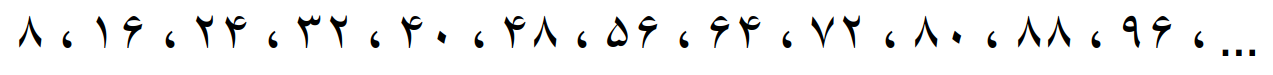
مضرب های 9
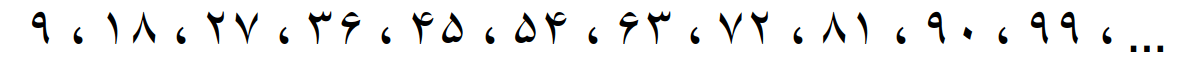
مضرب های 10
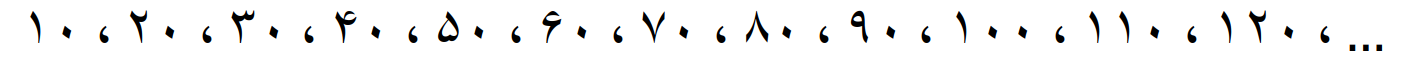
مضرب های 11
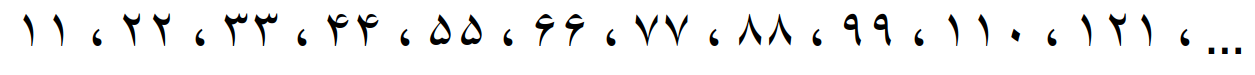
مضرب های مشترک دو عدد
اگر از ما خواسته باشند که مضرب های مشترک دو عدد را بنویسیم با نوشتن مضرب های هر کدام از این اعداد و مقایسه اعداد بدست آمده می توان مضارب مشترک آن ها را پیدا کرد
مثال 2
مضرب های مشترک دو عدد 3 و 4 را بنویسید
جواب:
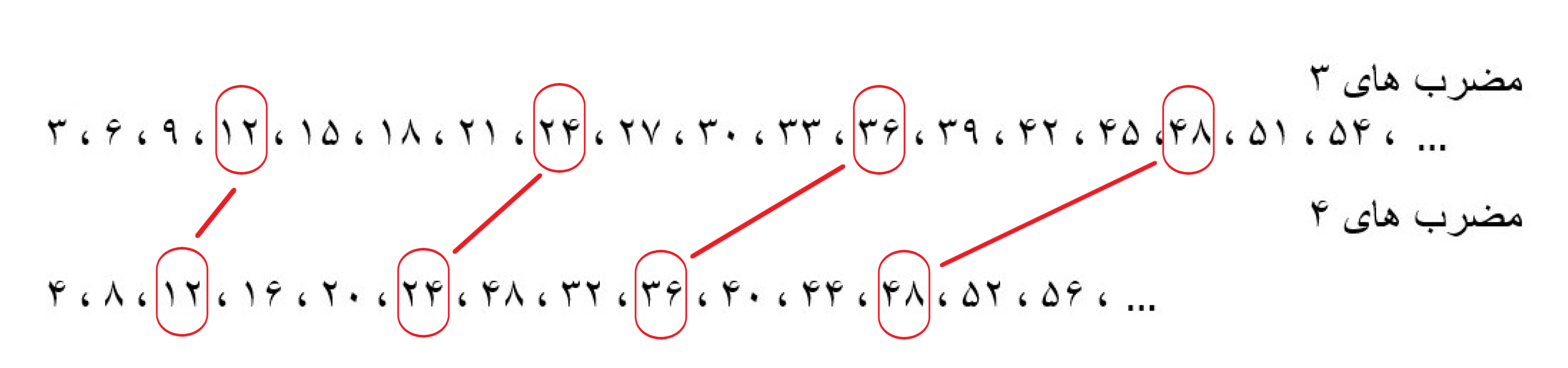
مضرب های مشترک دو عدد 3 و 4
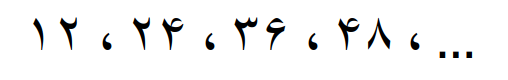
توجه داشته باشید که مضرب های مشترک دو عدد 3 و 4، تا بینهایت ادامه دارد
مثال 3
مضرب های مشترک دو عدد 10 و 15 را بنویسید
جواب:
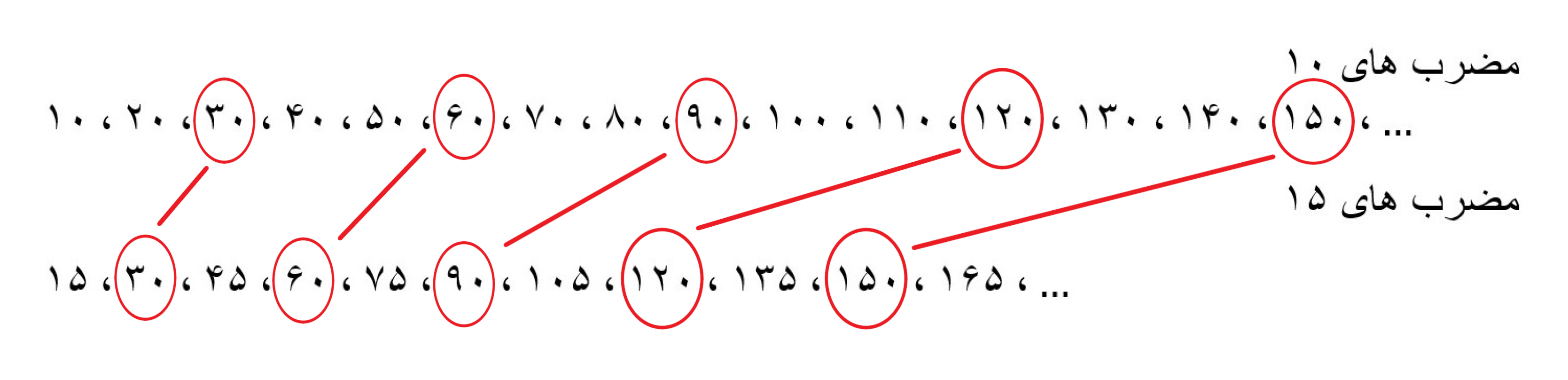
مضرب های مشترک دو عدد 10 و 15
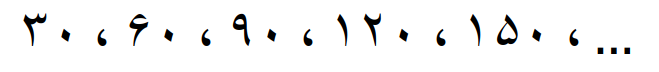
توجه داشته باشید که مضرب های مشترک دو عدد 10 و 15 تا بی نهایت ادامه دارد
مثال 4
دو عدد 3 و 15 چند مضرب مشترک کوچکتر از 61 دارند؟
جواب:
ابتدا مضارب کوچکتر از 61 دو عدد 3 و 15 را می نویسیم
مضرب های 3
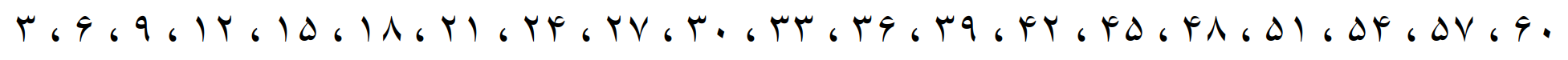
مضرب های 15
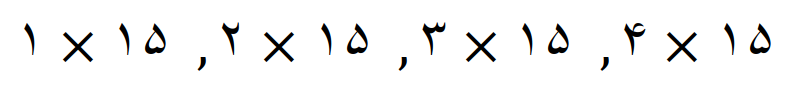
پس مضرب های 15 که کوچکتر از 61 هستند می شود
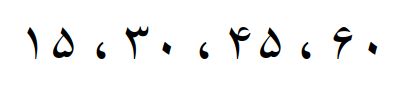
مضرب های مشترک دو عدد 3 و 15 که کوچکتر از 61 هستند
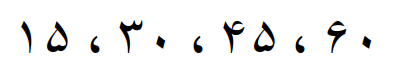
که همان مضارب 15 بدست می آید پس دو عدد 3 و 15 دارای چهار مضرب مشترک کوچکتر از 61 می باشند.
مثال 5
ششمین مضرب مشترک دو عدد 9 و 12 را بنویسید
جواب: ششمین مضرب مشترک، دو عدد 9 و 12 را از ما خواسته
ابتدا مضارب این دو عدد را نوشته و بعد مضرب های که در هر دو وجود دارد را مشخص می کنیم
مضرب های 9
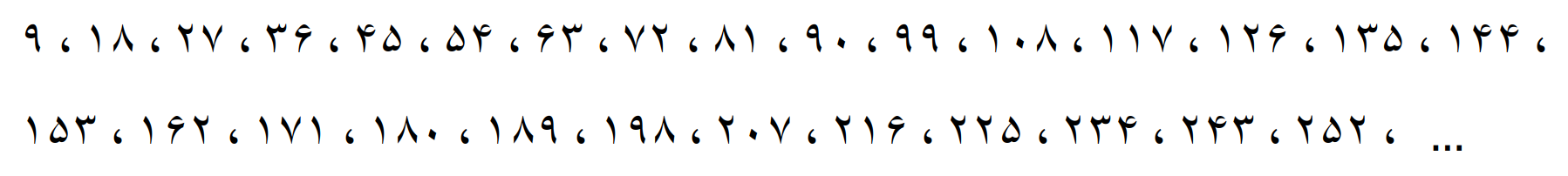
مضرب های 12
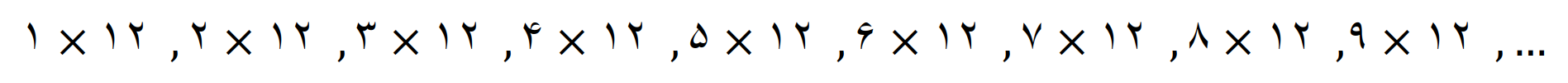
پس داریم
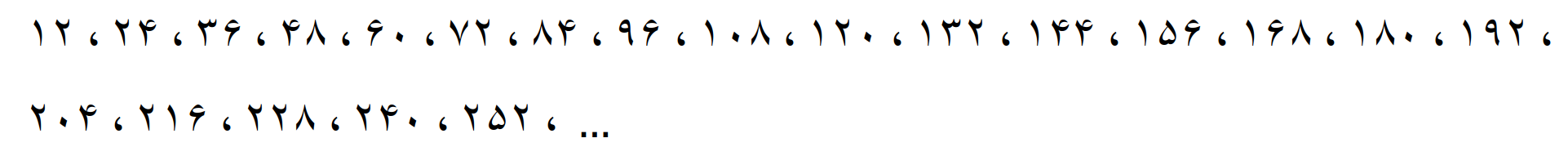
مضرب های مشترک دو عدد 9 و 12

بنابراین ششمین مضرب مشترک دو عدد 9 و 12، عدد 216 می باشد.
به نظر شما می توانیم بدون نوشتن مضرب های دو عدد، n مین مضرب مشترک آن دو عدد را محاسبه کنیم؟!
تمرین 1
40 مین(چهلمین) مضرب مشترک دو عدد 4 و 10 را بنویسید؟
توجه؛ دوباره به مضرب های مشترکی که در مثال های قبل بدست آوردیم، نگاه کنید
مضرب های مشترک دو عدد 3 و 4
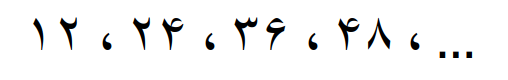
مضرب های مشترک دو عدد 10 و 15
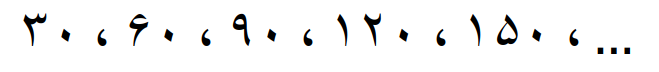
مضرب های مشترک دو عدد 3 و 15 که کوچکتر از 61 هستند
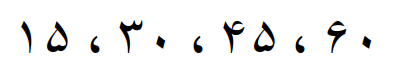
مضرب های مشترک دو عدد 9 و 12
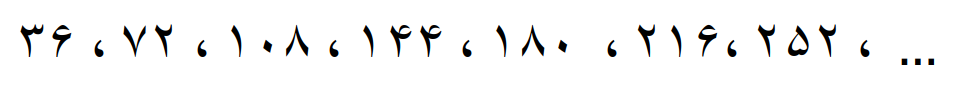
آیا بین مضرب های مشترک دو عدد، رابطه ای وجود دارد؟!
به مضرب های مشترک دو عدد 3 و 4 نگاه کنید
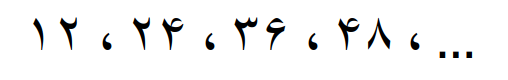
از عدد 12 شروع شده و ظاهراً اعداد مضرب 12 هستند
این موضوع را بررسی می کنیم
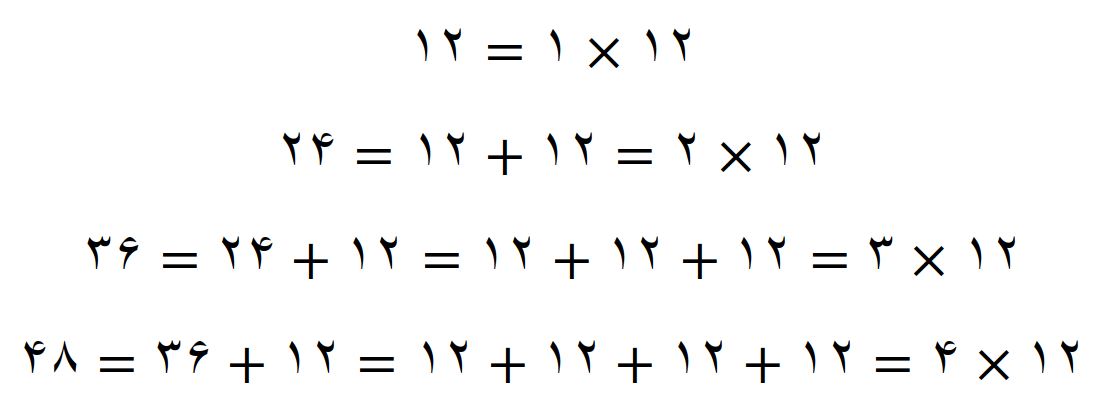
می بینیم که این اعداد مضارب 12 هستند
اگر مضرب های مشترک دو عدد 3 و 4 مضارب 12 باشند پس اعداد بعدی، باید عددهای زیر باشند
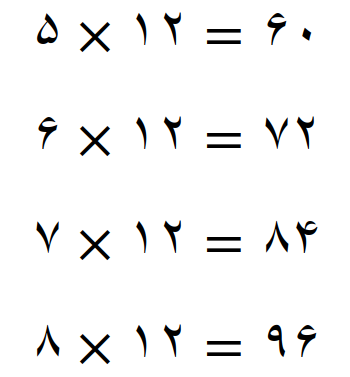
نوشتن مضرب های عدد 3 و عدد 4 را ادامه می دهیم تا ببینیم که اعداد 60، 72، 84 و 96 جزء مضارب این دو عدد هستند یا نه؟
مضرب های 3
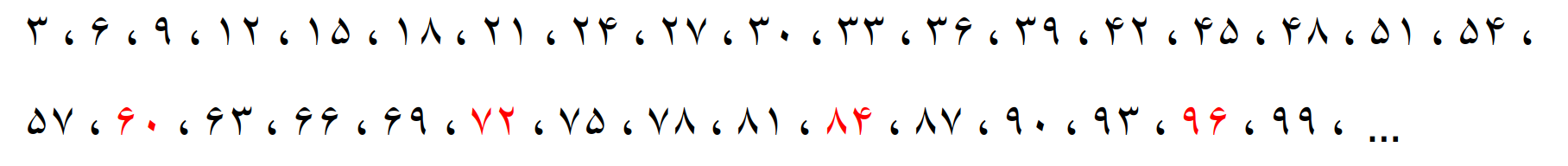
مضرب های 4
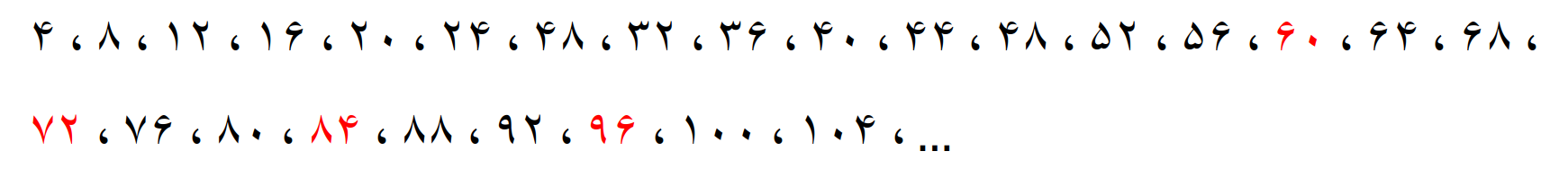
بنابراین معلوم می شود حدس ما درست بوده و مضرب های مشترک دو عدد 3 و 4 مضارب 12 هستند
به مضرب های مشترک دو عدد 10 و 15 نگاه کنید
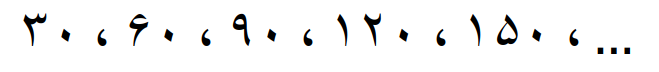
به نظر می رسد که مضرب های مشترک دو عدد 10 و 15، مضارب 30 هستند
این موضوع را بررسی می کنیم
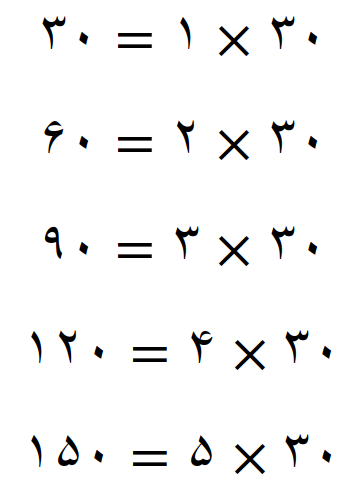
می بینیم که اعداد بالا مضرب 30 هستند حالا اعداد بعدی که مضرب 30 هستند را می نویسیم
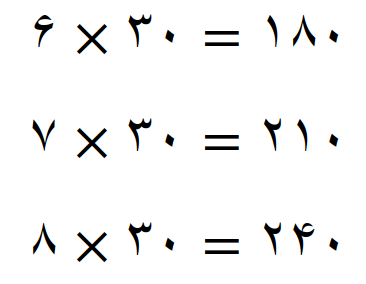
نوشتن مضرب های عدد 10 و عدد 15 را ادامه می دهیم تا ببینیم که اعداد 180، 210 و 240 جزء مضارب این دو عدد هستند یا نه؟
مضرب های 10
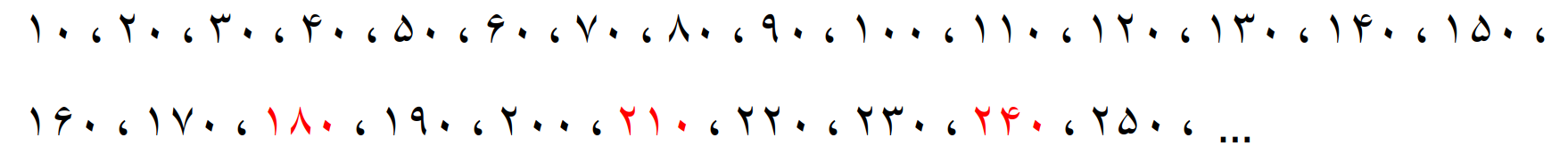
مضرب های 15
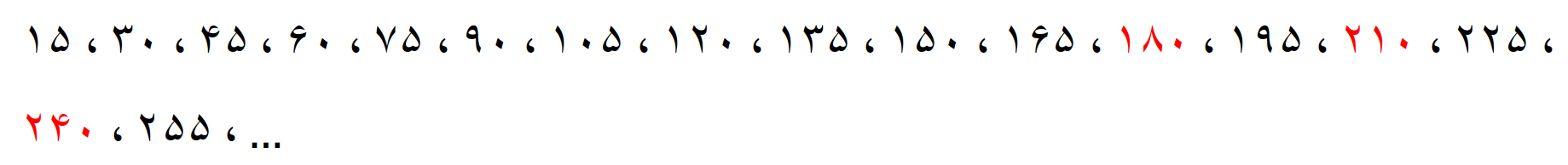
بنابراین معلوم می شود حدس ما درست بوده و مضرب های مشترک دو عدد 10 و 15، مضارب 30 هستند
مضرب های مشترک دو عدد 3 و 15 که کوچکتر از 61 هستند
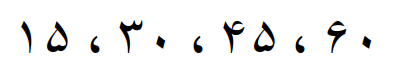
این اعداد نیز مضرب 15 هستند
مضرب های مشترک دو عدد 9 و 12
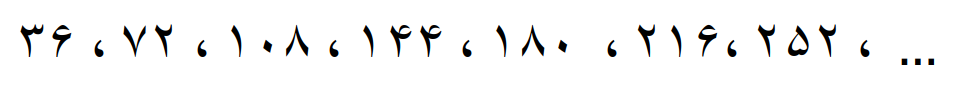
با عدد 36 شروع شده و عددهای بعدی نیز مضرب 36 هستند
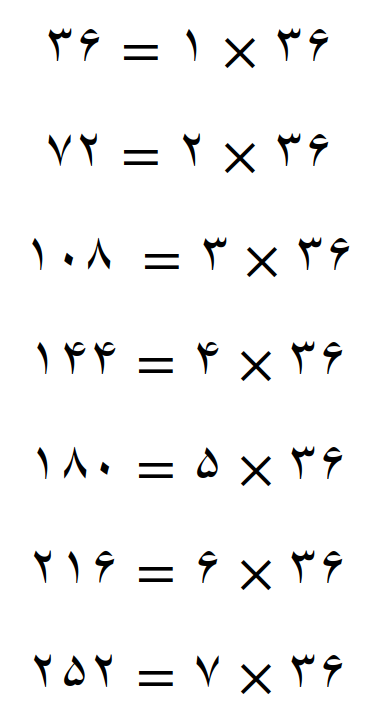
بنابراین مضرب های مشترک دو عدد 9 و 12 مضارب عدد 36 هستند
به توضیحات گفته شده در بالا توجه کنید،
12 اولین مضرب مشترک دو عدد 3 و 4 است و همچنین 12 کوچکترین مضرب مشترک این دو عدد می باشد و سایر مضرب های مشترک این دو عدد، مضارب 12 هستند.
30 اولین مضرب مشترک دو عدد 10 و 15 است و همچنین 30 کوچکترین مضرب مشترک این دو عدد می باشد و سایر مضرب های مشترک این دو عدد، مضارب 30 هستند.
15 اولین مضرب مشترک دو عدد 3 و 15 است و همچنین 15 کوچکترین مضرب مشترک این دو عدد می باشد و سایر مضرب های مشترک این دو عدد، مضارب 15 هستند.
36 اولین مضرب مشترک دو عدد 9 و 12 است و همچنین 36 کوچکترین مضرب مشترک این دو عدد می باشد و سایر مضرب های مشترک این دو عدد، مضارب 36 هستند.
نتیجه
1- مضرب های مشترک دو عدد، مضارب “اولین مضرب مشترک” آن دو عدد هستند؛ یعنی اینکه اگر ما بتوانیم با روشی اولین مضرب مشترک دو عدد را پیدا کنیم سایر مضارب مشترک آن دو عدد، از ضرب اولین مضرب مشترک در اعداد طبیعی بدست می آید.
2- اولین مضرب مشترک دو عدد، “کوچکترین مضرب مشترک” آن دو عدد است.
3- اگراز ما بپرسند n مین مضرب مشترک دو عدد را بنویسیم کافی است اولین مضرب مشترک دو عدد را پیدا کرده و آن را در n ضرب کنیم، حاصل n مین مضرب مشترک آن دو عدد خواهد بود(n یک عدد است).
مضرب های مشترک سه عدد یا بیش از آن
ابتدا مضرب های آن عددها را نوشته و بعد نتایج را با هم مقایسه کرده و عددهای که مشترک هستند را می نویسیم این عددهای یکسانی که در مضارب آن عددها وجود دارد، مضرب های مشترک آن ها می باشند.
مثال 6
مضرب های مشترک سه عدد 6 ، 8 و 16 را بنویسید
جواب: ابتدا مضارب این اعداد را می نویسیم و بعد از آن بررسی می کنیم کدام مضرب ها در هر سه آن ها وجود دارد(نگاه می کنیم به عددها که نوشتیم و آن های که در هر سه این مضارب تکرار شده را می نویسیم)
مضرب های 6
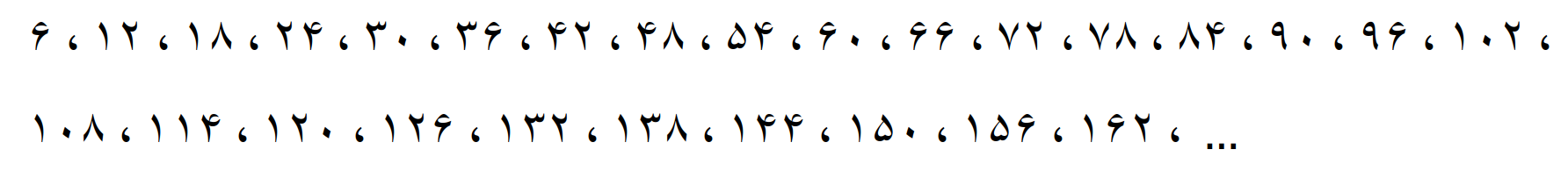
مضرب های 8
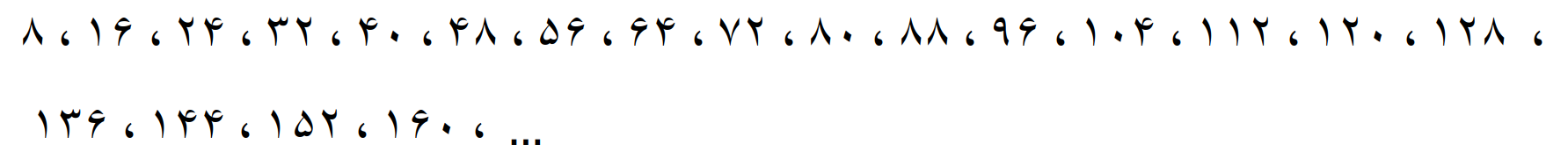
مضرب های 16
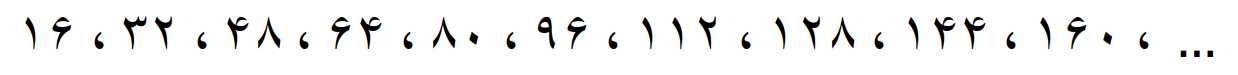
مضرب های عدد 16 را با مضرب های دو عدد 6 و 8 مقایسه می کنیم تا مضرب های مشترک این سه عدد را پیدا کنیم
عددهای 16 و 32 مضرب 16 و هم مضرب 8 هستند ولی مضرب 6 نیستند
عدد 48 مضرب 16 هست که جزء مضرب های عدد 6 و 8 نیز می باشد پس 48 مضرب مشترک این سه عدد است
عددهای 64 و 80 مضرب 16 و هم مضرب 8 هستند ولی مضرب 6 نیستند
عدد 96 مضرب 16 هست که جزء مضرب های عدد 6 و 8 نیز می باشد پس 96 مضرب مشترک این سه عدد است
عددهای 112 و 128 مضرب 16 و هم مضرب 8 هستند ولی مضرب 6 نیستند
عدد 144 مضرب 16 هست که جزء مضرب های عدد 6 و 8 نیز می باشد پس 144 مضرب مشترک این سه عدد است
عدد 160 مضرب 16 و هم مضرب 8 هست ولی مضرب 6 نیست
بنابراین مضارب مشترک سه عدد 6 ، 8 و 16
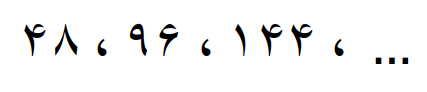
کوچکترین مضرب مشترک
اولین مضرب مشترک دو عدد(یا سه عدد یا بیشتر)، “کوچکترین مضرب مشترک” آن عددها است.
روش های بدست آوردن کوچکترین مضرب مشترک
روش اول
یک روش برای بدست آوردن کوچکترین مضرب مشترک(Least common multiple) نوشتن مضارب آن چند عدد و مشخص کردن مضرب های مشترک آن عددها است، که اولین مضرب مشترک آن ها، کوچکترین مضرب مشترک آن عددها خواهد بود(در مثال های قبل این روش را دیدید).
مثلاً در مثال 6
مضارب مشترک سه عدد 6 ، 8 و 16
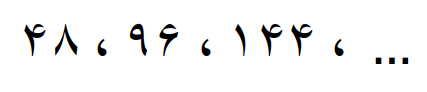
بدست آمد، که در آن عدد 48 اولین مضرب مشترک این سه عدد هست بنابراین عدد 48 کوچکترین مضرب مشترک سه عدد 6 ، 8 و 16 می باشد.
روش دوم
برای یافتن کوچکترین مضرب مشترک چند عدد، ابتدا این عددها را به عامل های اول تجزیه کرده و بعد عامل های مشترک این عدد ها را با توان بیشتر در عامل های غیر مشترک این عددها ضرب می کنیم، حاصل کوچکترین مضرب مشترک آن ها خواهد بود.
مثلاً کوچکترین مضرب مشترک سه عدد 6 ، 8 و 16 را با این روش بدست می آوریم
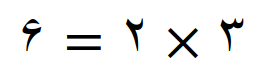
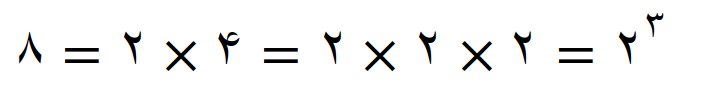
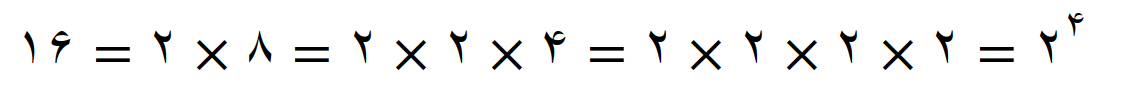
پس نتیجه تجزیه به صورت زیر است
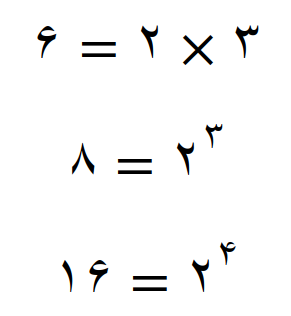
عامل های اول بدست آمده را با هم مقایسه می کنیم بین این عامل های اول، عامل اول 2 مشترک است در حالی که عامل اول 3، تنها در تجزیه عدد 6 دیده می شود
پس عامل غیر مشترک این عددها، عدد 3 هست آن را می نویسیم

در مورد عامل مشترک(عدد 2) این عددها، باید آن که توانش عدد بزرگتری هست را بنویسیم بین
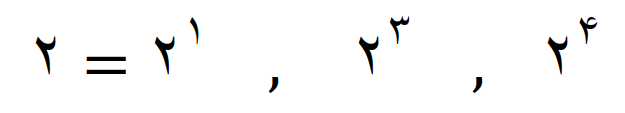
2 به توان 4، توانش بزرگتر است پس داریم

در نتیجه
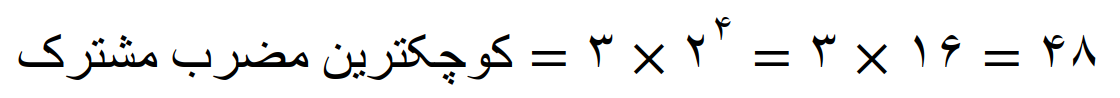
بنابراین عدد 48 کوچکترین مضرب مشترک سه عدد 6 ، 8 و 16 می باشد.
البته برای تجزیه عدد می توانید از روش های تجزیه درختی و تجزیه ستونی استفاده کنید
مثال 7
عدد های 27 و 36 را به روش ستونی تجزیه کرده و سپس کوچکترین مضرب مشترک آن ها را بنویسید
جواب:
تجزیه 27
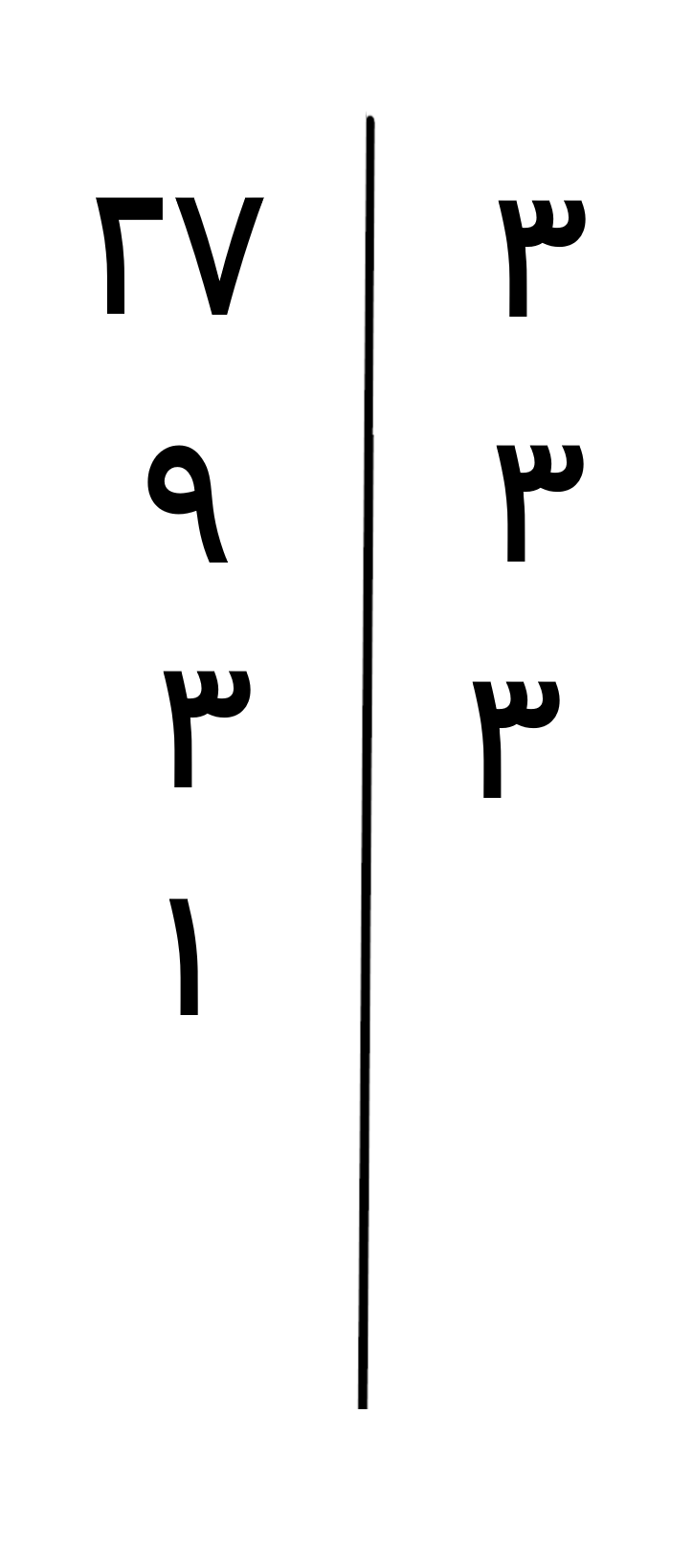
تجزیه 36
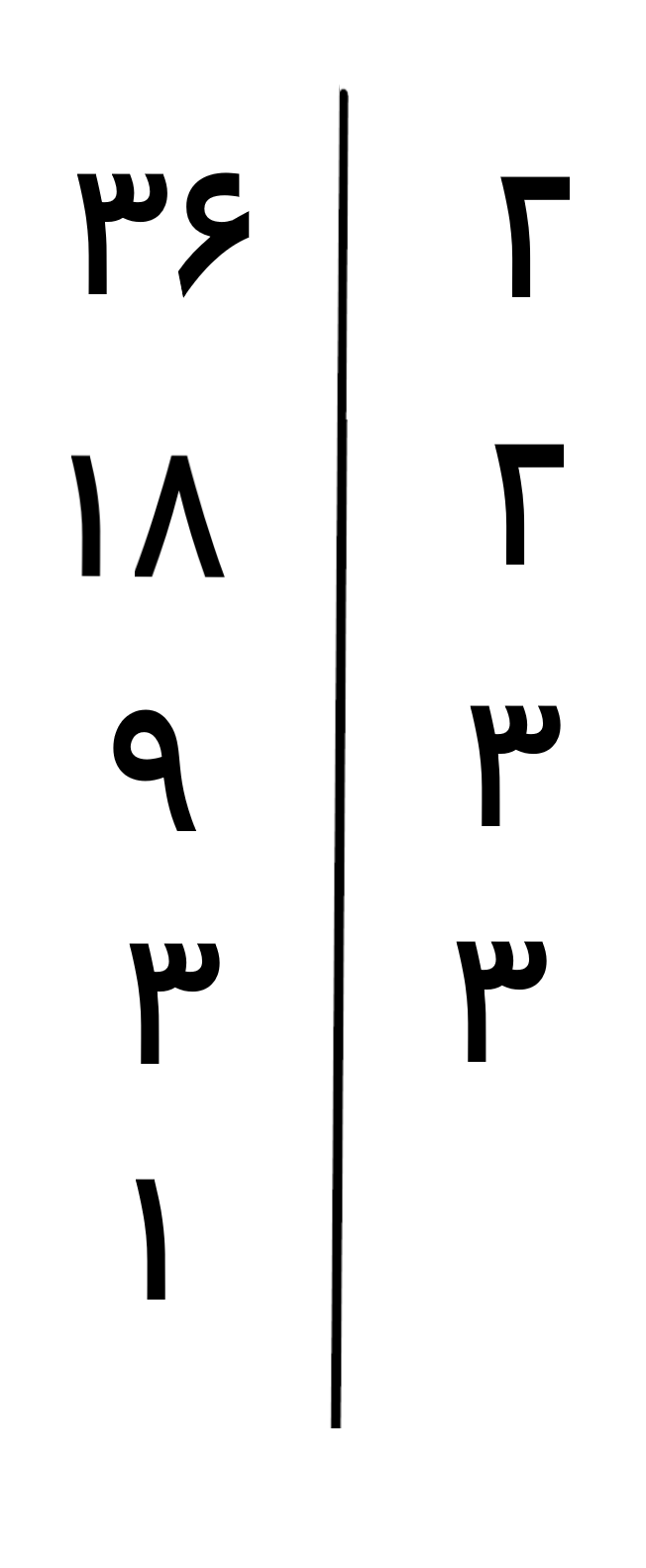
اگر با مفهوم اعداد توان دار آشنا نیستید می توانید به این صورت عمل کنید،
تجزیه عددها(عامل های اول) را در ردیف های روبروی هم به صورتی می نویسیم که عددهای یکسان جلوی یکدیگر قرار بگیرند(البته هر عدد تنها روبروی یک عدد دیگر قرار می گیرد) به تصویر نگاه کنید
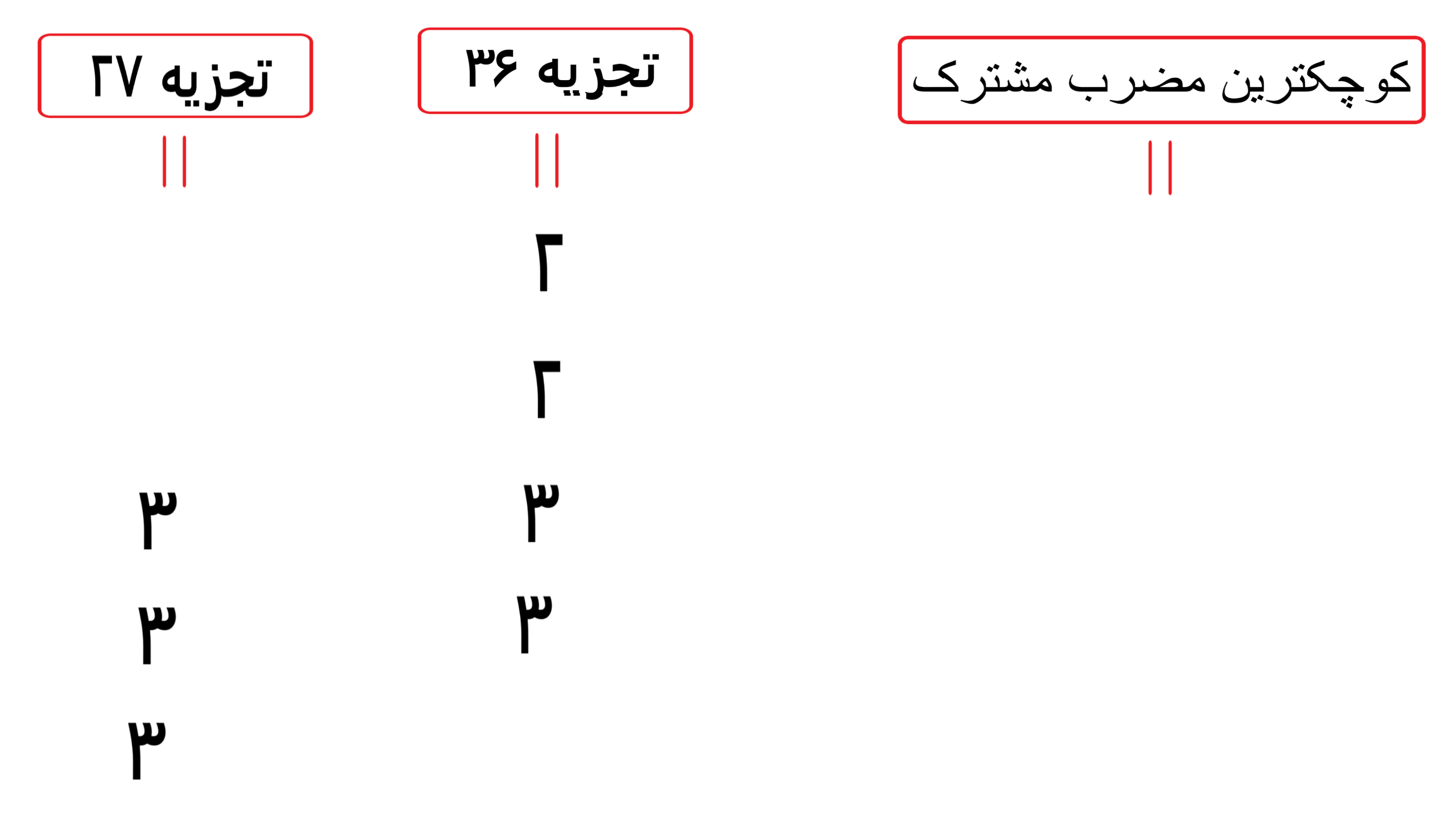
بعد عددهای را که روبروی آن ها عددی هست و هم عدد های که مقابل آن ها(قبل یا بعد آن) عددی نیست را در زیر عبارت “کوچکترین مضرب مشترک” می نویسیم کوچکترین مضرب مشترک مساوی است با حاصلضرب این عددها.
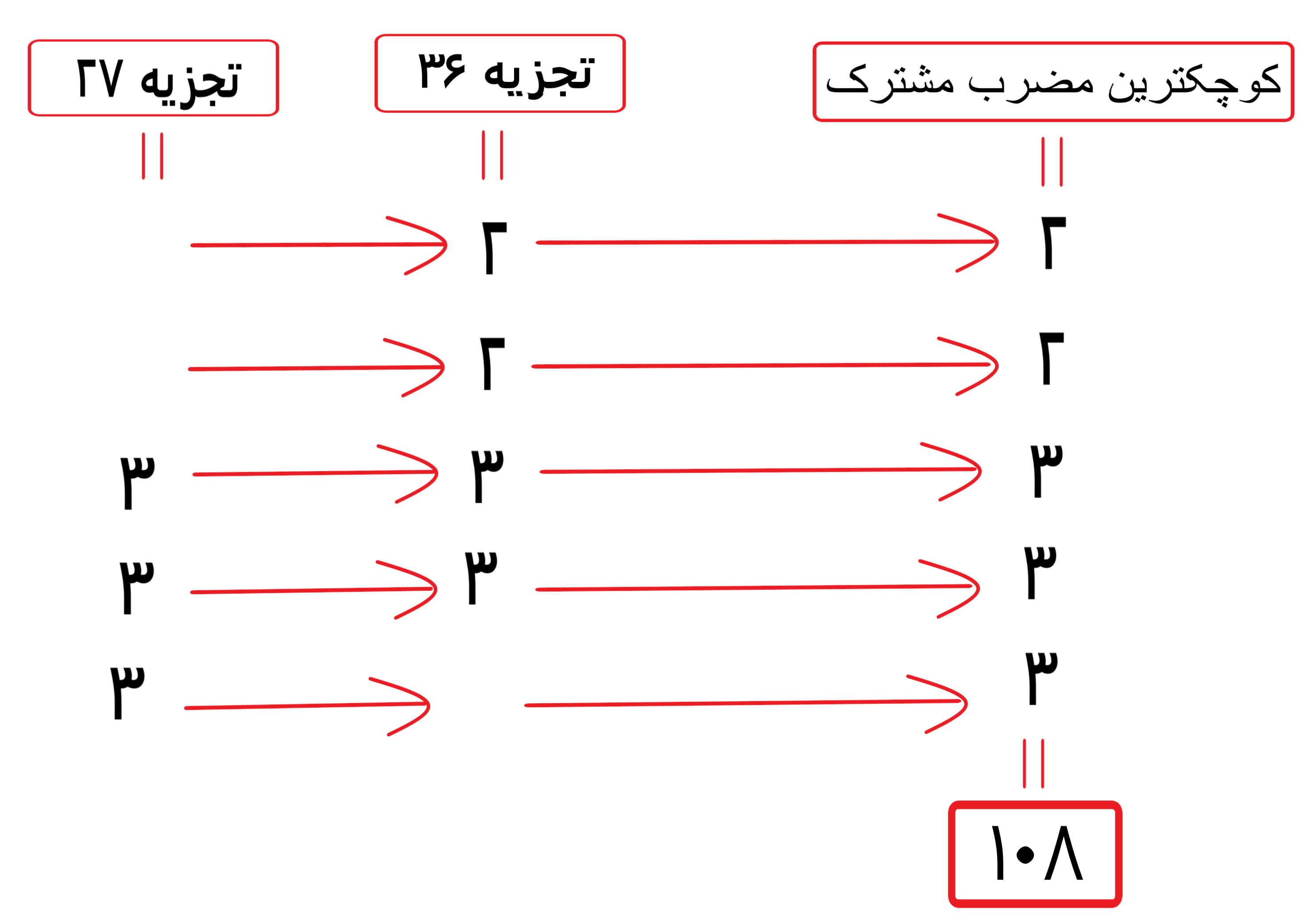
کوچکترین مضرب مشترک 27 و 36 مساوی است با 108
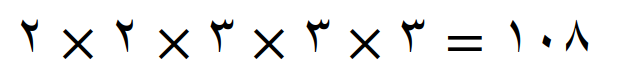
با استفاده از مفهوم اعداد توان دار کوچکترین مضرب مشترک 27 و 36 را پیدا می کنیم
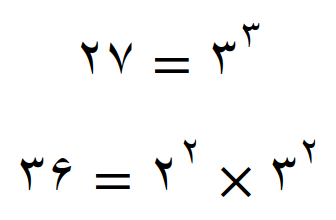
کوچکترین مضرب مشترک مساوی است با، عامل های مشترک با توان بیشتر ضربدر عامل های غیر مشترک

مثال 8
عدد های 42 و 45 را به روش درختی تجزیه کرده و سپس کوچکترین مضرب مشترک آن ها را بنویسید
جواب:
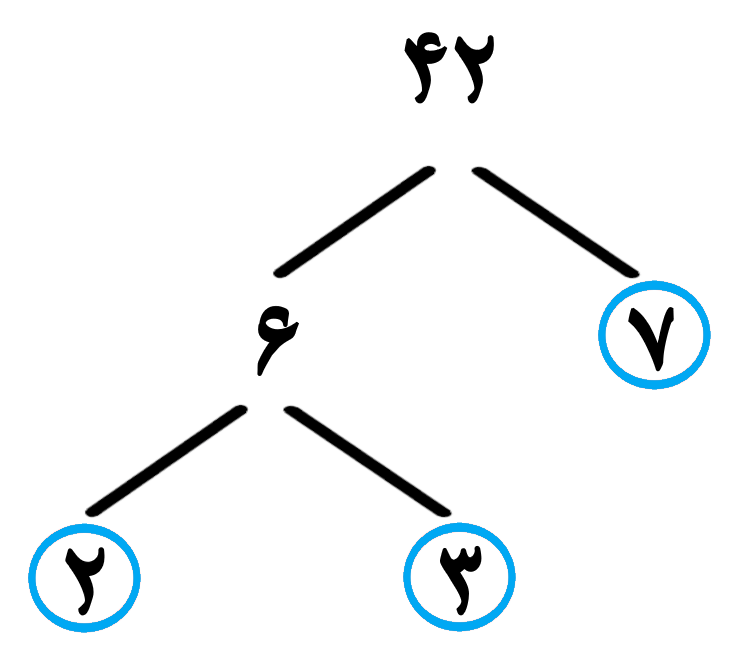
تجزیه 42
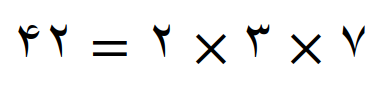
تجزیه 45
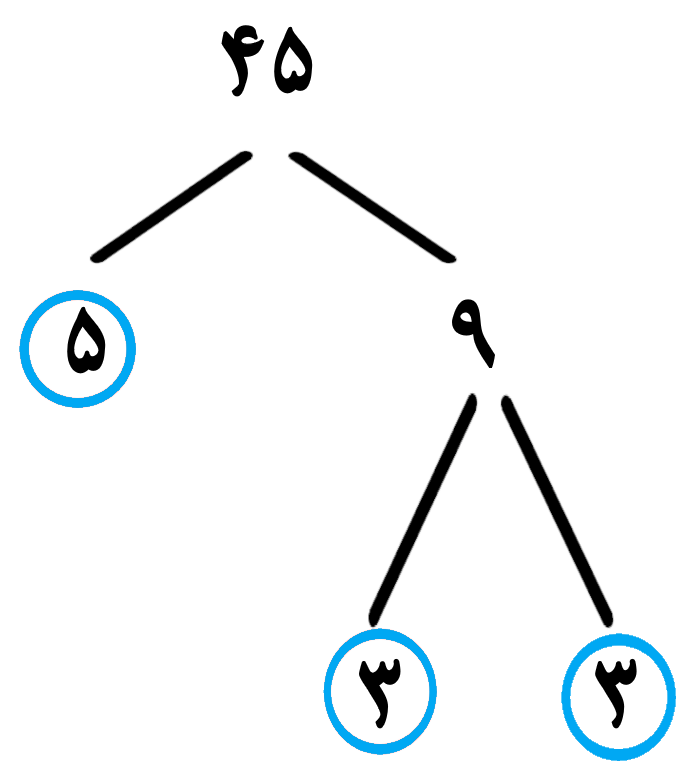
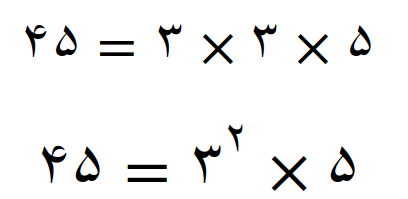
اگر با مفهوم اعداد توان دار آشنا نیستید به این صورت عمل کنید،
تجزیه عددها را در ردیف های روبروی هم به صورتی می نویسیم که عددهای یکسان جلوی یکدیگر قرار بگیرند
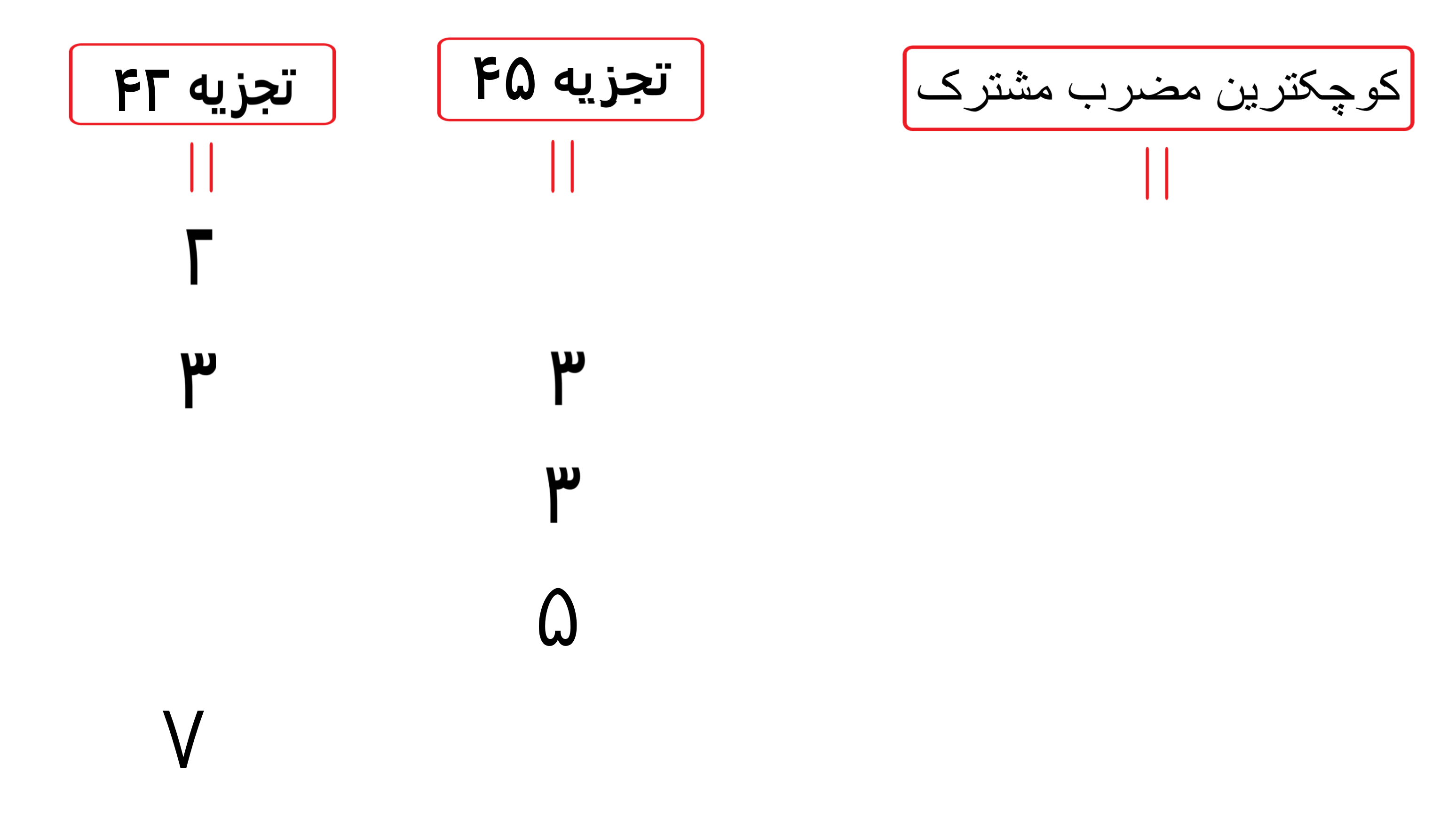
حاصل را بدست می آوریم؛ عددهای را که روبروی آن ها عددی هست و هم عدد های که مقابل آن ها عددی نیست را در زیر عبارت “کوچکترین مضرب مشترک” می نویسیم
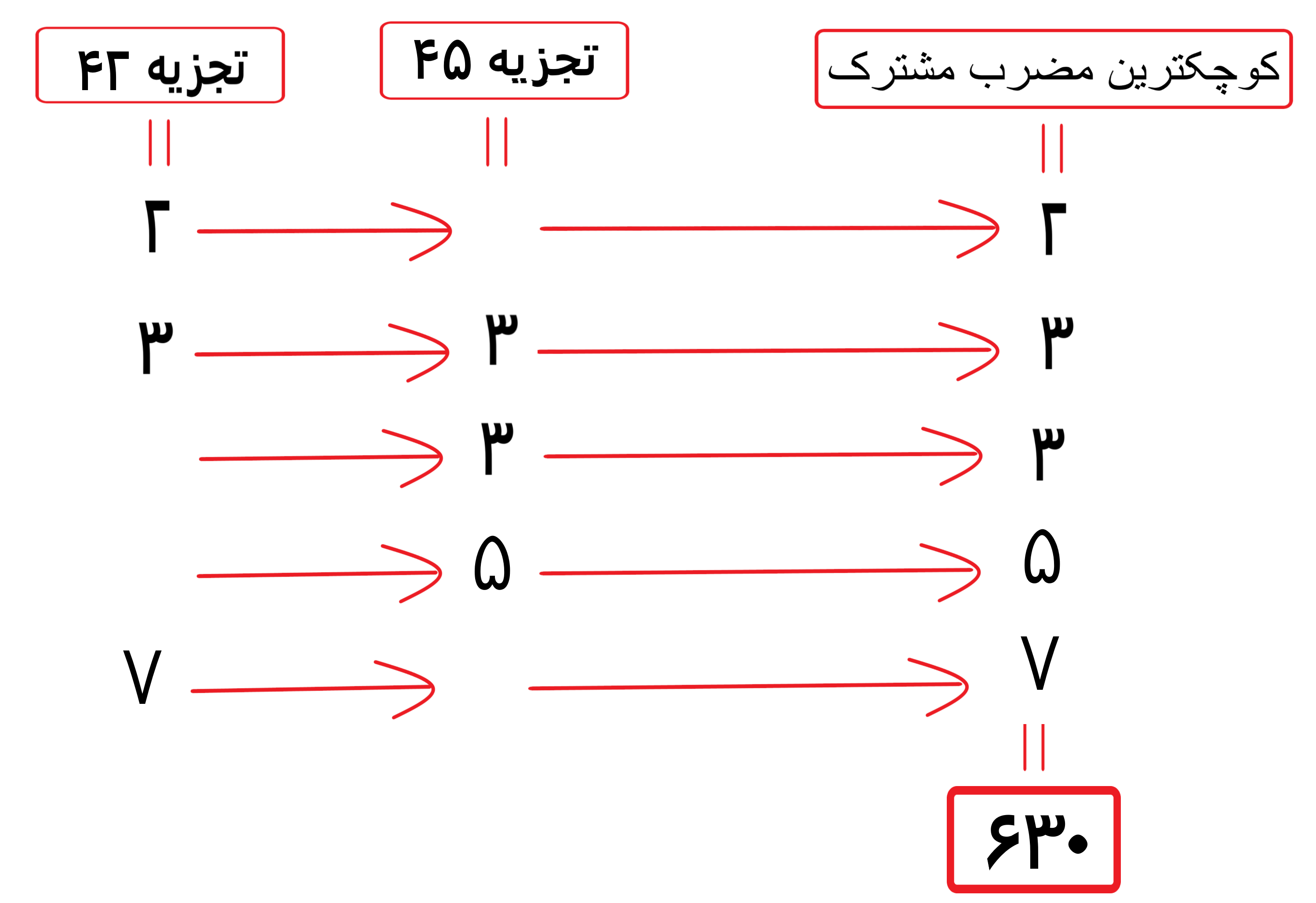
کوچکترین مضرب مشترک مساوی است با حاصلضرب این عددها
کوچکترین مضرب مشترک 42 و 45 مساوی است با 630
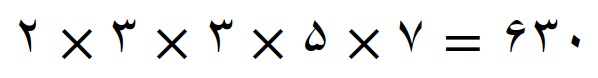
با استفاده از مفهوم اعداد توان دار کوچکترین مضرب مشترک 42 و 45 را پیدا می کنیم
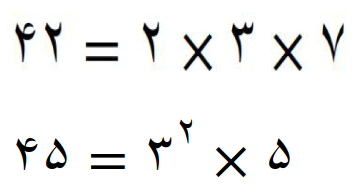
کوچکترین مضرب مشترک مساوی است با، عامل های مشترک با توان بیشتر ضربدر عامل های غیر مشترک
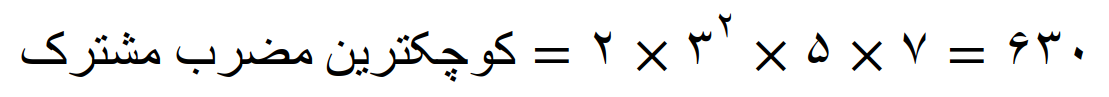
مثال 9
کوچکترین مضرب مشترک عدد های 15 و 60 را بیابید
جواب:
تجزیه عدد 15
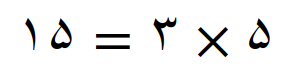
تجزیه عدد 60
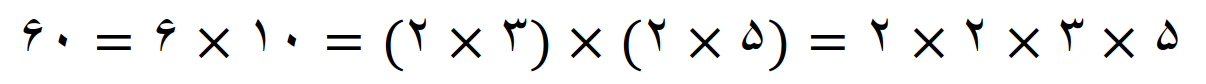
یا
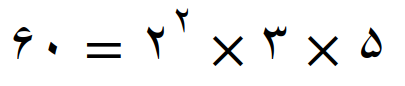
اگر با مفهوم اعداد توان دار آشنا نیستید به این صورت عمل کنید،
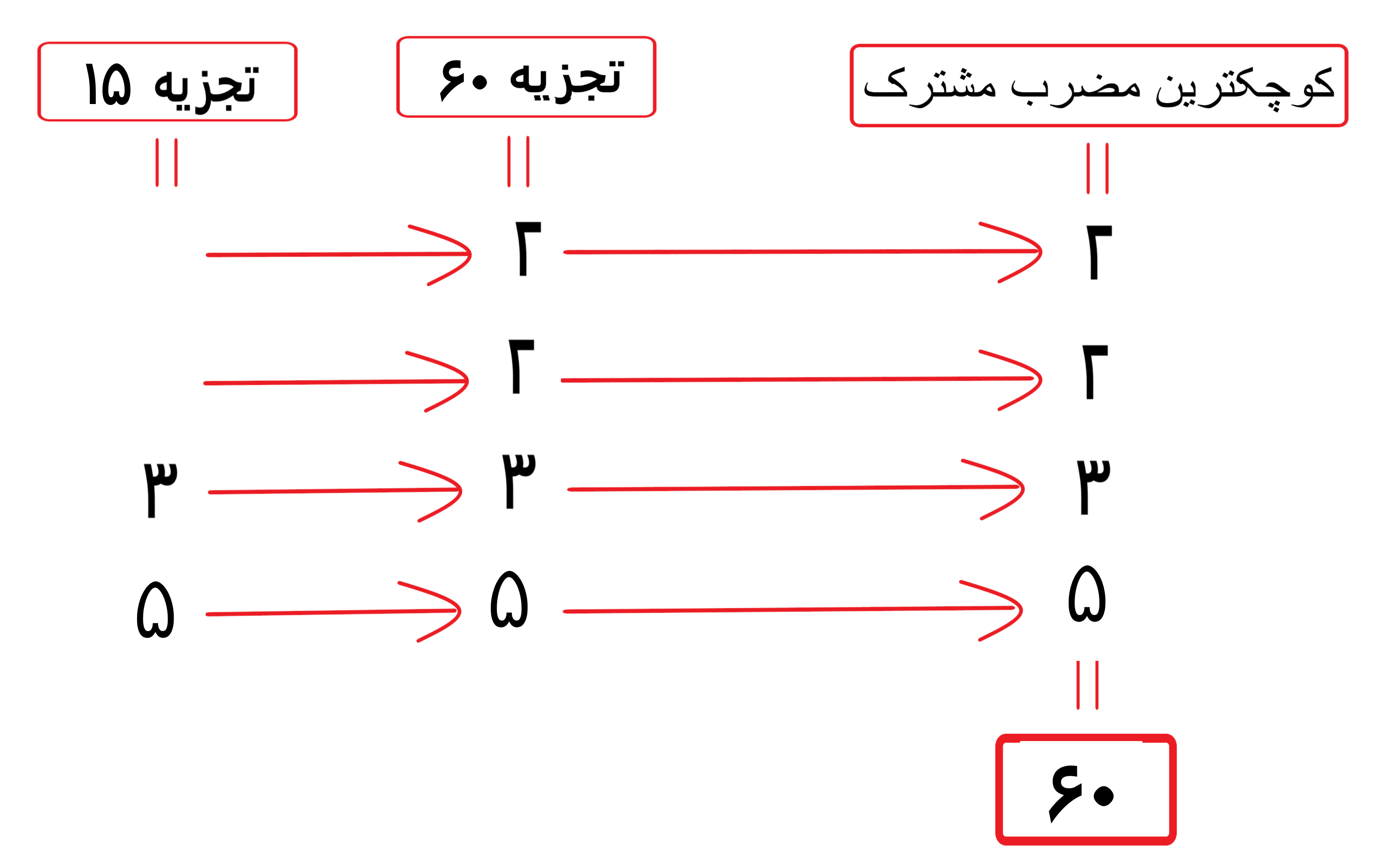
کوچکترین مضرب مشترک 15 و 60 مساوی است با 60
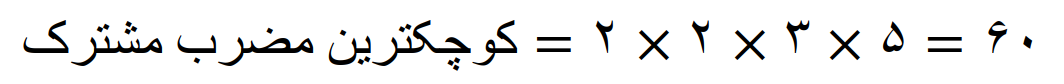
با استفاده از مفهوم اعداد توان دار کوچکترین مضرب مشترک 15 و 60 را پیدا می کنیم
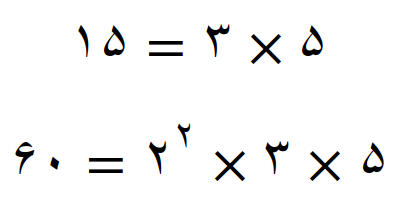
کوچکترین مضرب مشترک مساوی است با، عامل های مشترک با توان بیشتر ضربدر عامل های غیر مشترک
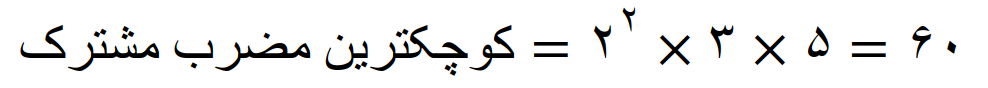
می بینیم که عدد 60 بر 15 بخش پذیر است و کوچکترین مضرب مشترک 15 و 60 نیز خود عدد 60 است
مثال 10
کوچکترین مضرب مشترک عددهای 13 و 78 را پیدا کنید
جواب:
تجزیه عدد 13
13 عددی اول است و قابل تجزیه نیست
تجزیه عدد 78
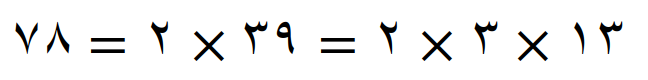
کوچکترین مضرب مشترک عدد های 13 و 78
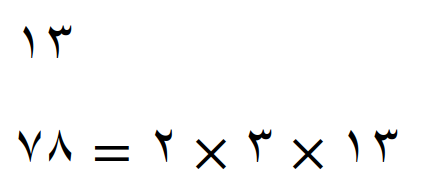
پس عدد 13 عامل مشترک و دو عدد 2 و 3 عامل های غیر مشترک هستند در نتیجه
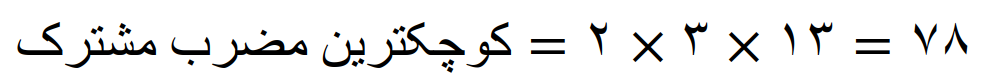
می بینیم که عدد 78 بر 13 بخش پذیر است و کوچکترین مضرب مشترک 13 و 78 نیز خود عدد 78 است
نکته 1
اگر دو عدد بر هم بخش پذیر باشند آن وقت کوچکترین مضرب مشترک آن ها مساوی است با عدد بزرگتر.
مثلاً عدد 24 بر 4 بخشپذیر است که از آن نتیجه می شود کوچکترین مضرب مشترک آن ها مساوی است با عدد 24
مثال 11
کوچکترین مضرب مشترک عددهای 97 و 149 را پیدا کنید
جواب:
عدد های 97 و 149 عدد اول هستند پس تجزیه پذیر نیستند
در نتیجه عامل مشترکی ندارند و اعداد 97 و 149 عامل های غیر مشترک آن ها است
بنابراین کوچکترین مضرب مشترک اعداد 97 و 149 مساوی است با، حاصل ضرب عامل های غیر مشترک آن ها
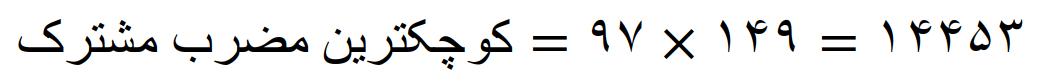
تمرین 2
نشان دهید که اعداد 97 و 149 عدد اول هستند
نکته 2
کوچکترین مضرب مشترک دو عددی که عدد اول هستند مساوی است با حاصل ضرب آن دو عدد.
مثال 12
کوچکترین مضرب مشترک اعداد زیر را بنویسید
20 و 21
22 و 23
24 و 25
جواب:
کوچکترین مضرب مشترک عددها 20 و 21
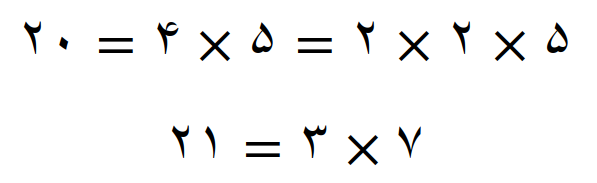
همه عامل های اول این دو عدد غیر مشترک هستند پس داریم
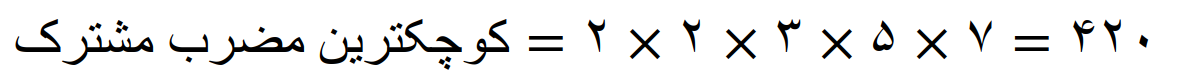
می بینیم که، کوچکترین مضرب مشترک عددها 20 و 21 مساوی است با حاصلضرب این دو عدد
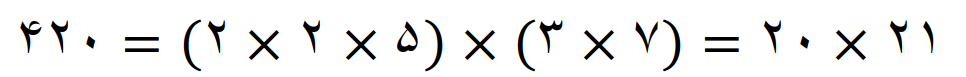
کوچکترین مضرب مشترک عددها 22 و 23
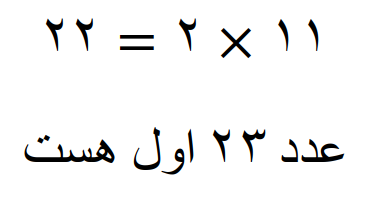
همه عامل های اول این دو عدد غیر مشترک هستند پس داریم
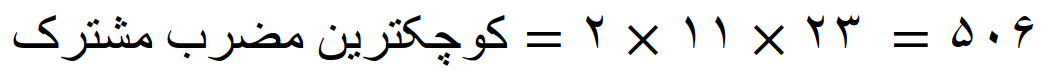
می بینیم که، کوچکترین مضرب مشترک عددها 22 و 23 مساوی است با حاصلضرب این دو عدد
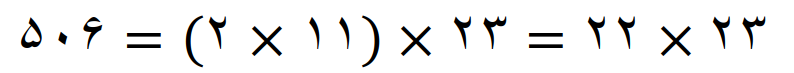
کوچکترین مضرب مشترک عددها 24 و 25
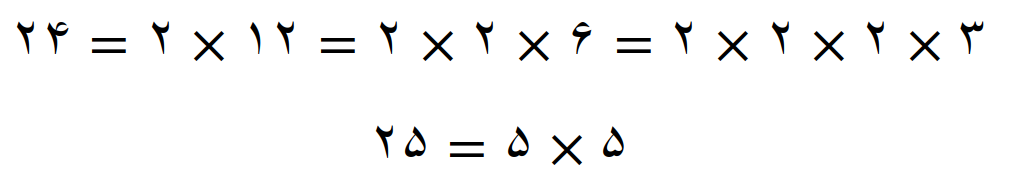
همه عامل های اول این دو عدد غیر مشترک هستند پس داریم
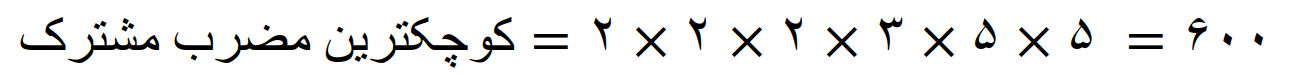
می بینیم که، کوچکترین مضرب مشترک عددها 24 و 25 مساوی است با حاصلضرب این دو عدد
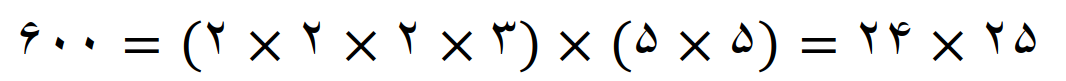
نکته 3
کوچکترین مضرب مشترک دو عدد متوالی، مساوی است با حاصل ضرب آن دو عدد.
مثال 13
کوچکترین مضرب مشترک سه عدد 35، 42 و 50 را بنویسید
جواب:
تجزیه عددها
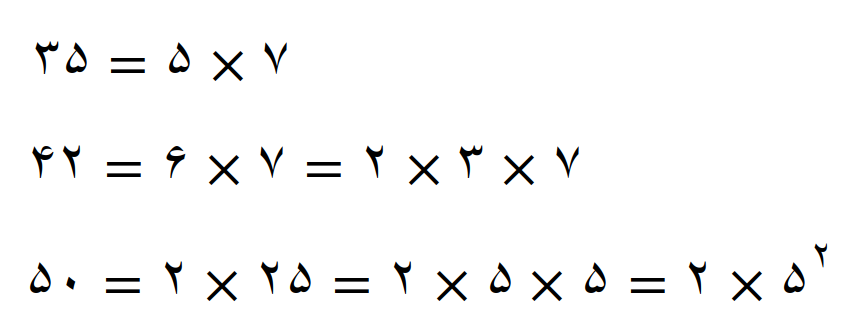
کوچکترین مضرب مشترک
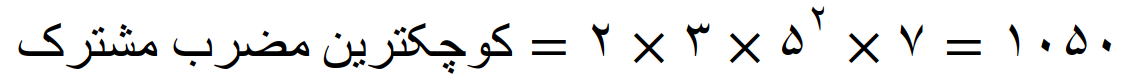
مثال 14
کوچکترین مضرب مشترک سه عدد 75، 81 و 90 را بنویسید
جواب:
تجزیه عددها
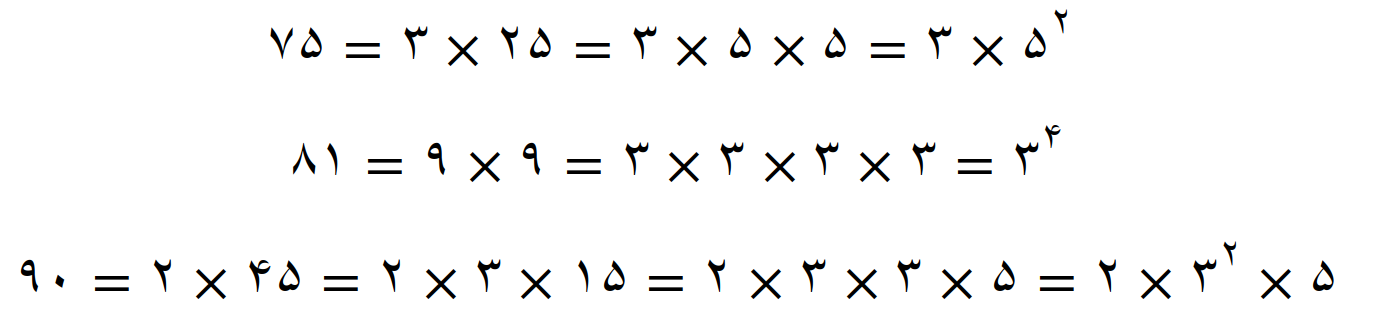
کوچکترین مضرب مشترک
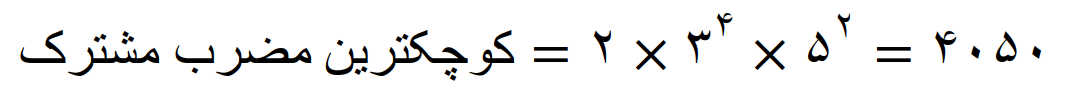
یا
به صورت زیر عمل کنید
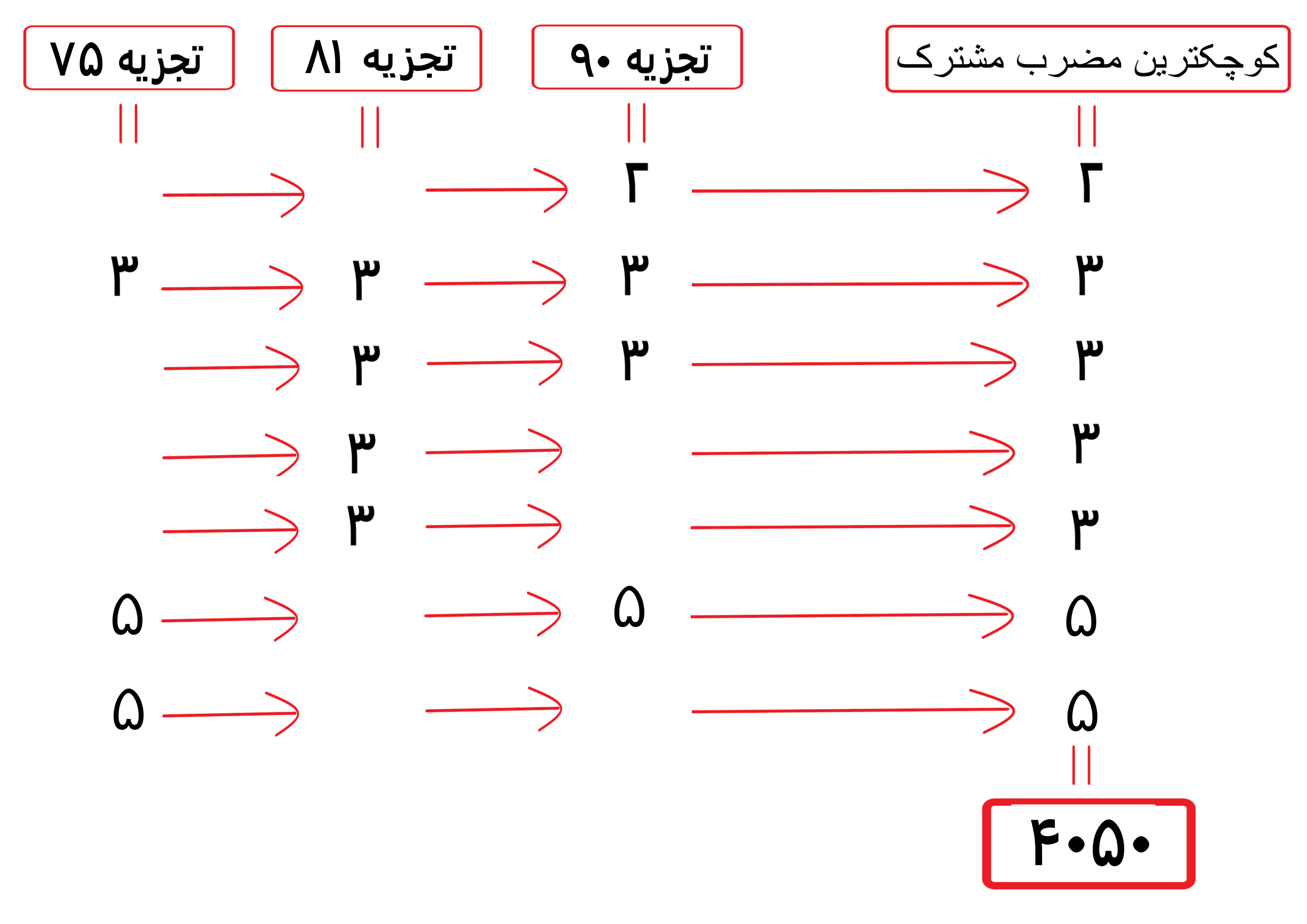
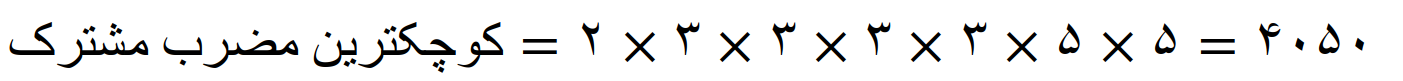
مثال 15
99 مین مضرب مشترک سه عدد 48، 160 و 360 را بنویسید
جواب: برای نوشتن نود و نهمین مضرب مشترک این سه عدد ما باید، ابتدا اولین مضرب مشترک آن ها را پیدا کنیم
دقت کنید؛ اولین مضرب مشترک چند عدد، کوچکترین مضرب مشترک آن اعداد است بنابراین ما باید با تجزیه عددها، کوچکترین مضرب مشترک آن ها را محاسبه کنیم
تجزیه عدد 48
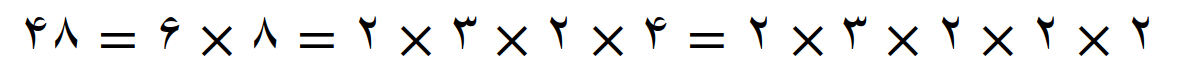
پس تجزیه عدد 48 می شود
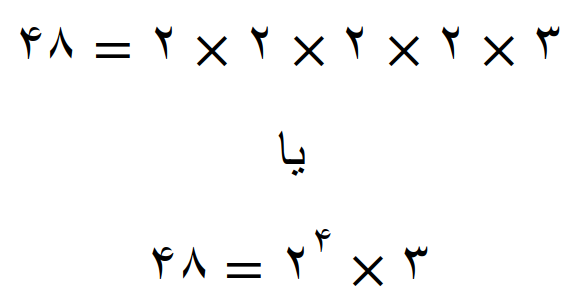
تجزیه عدد 160
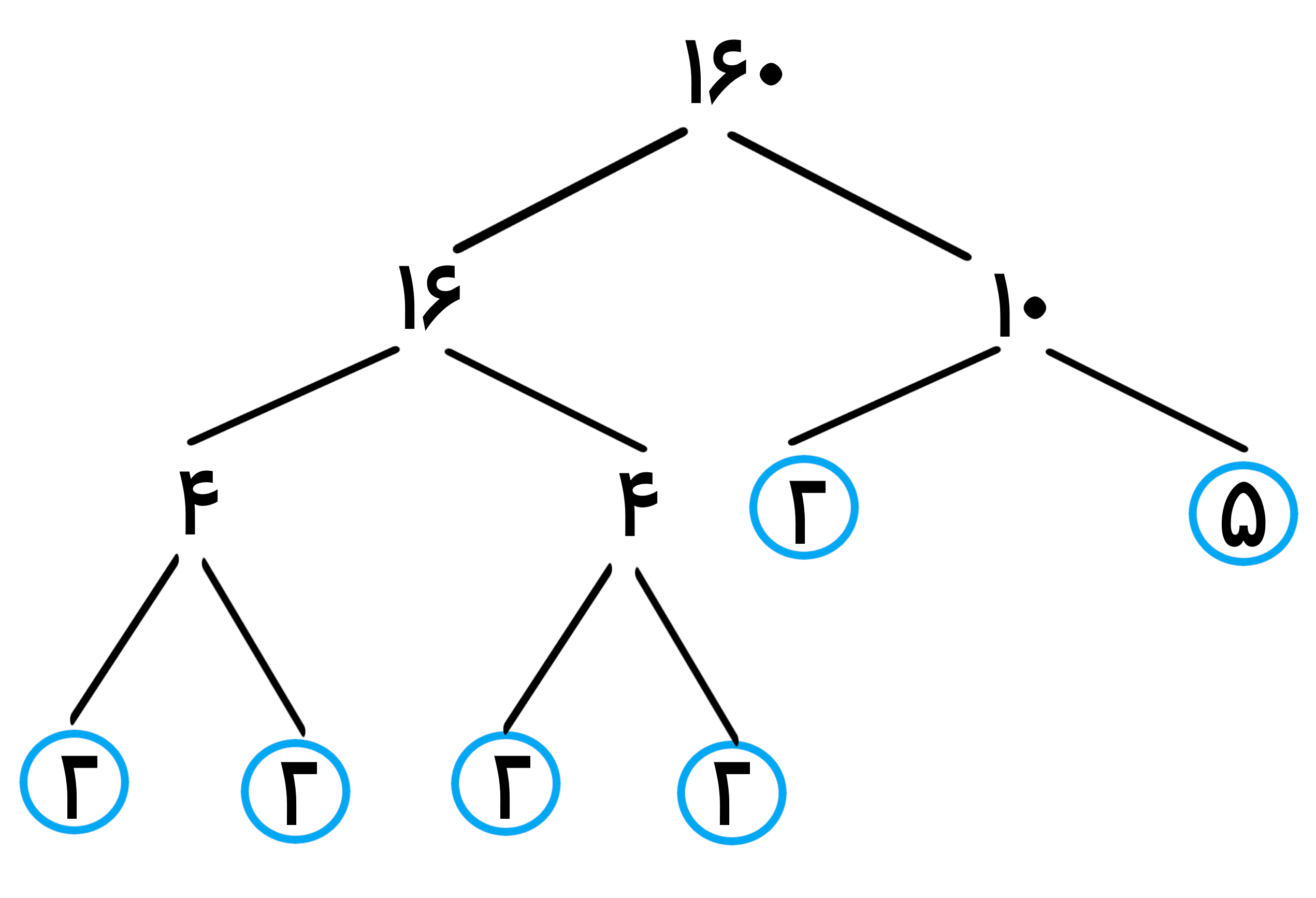
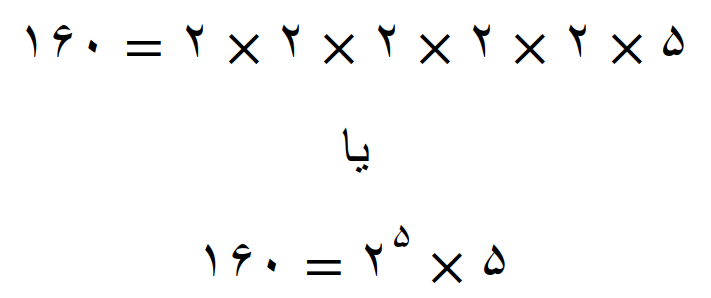
تجزیه عدد 360
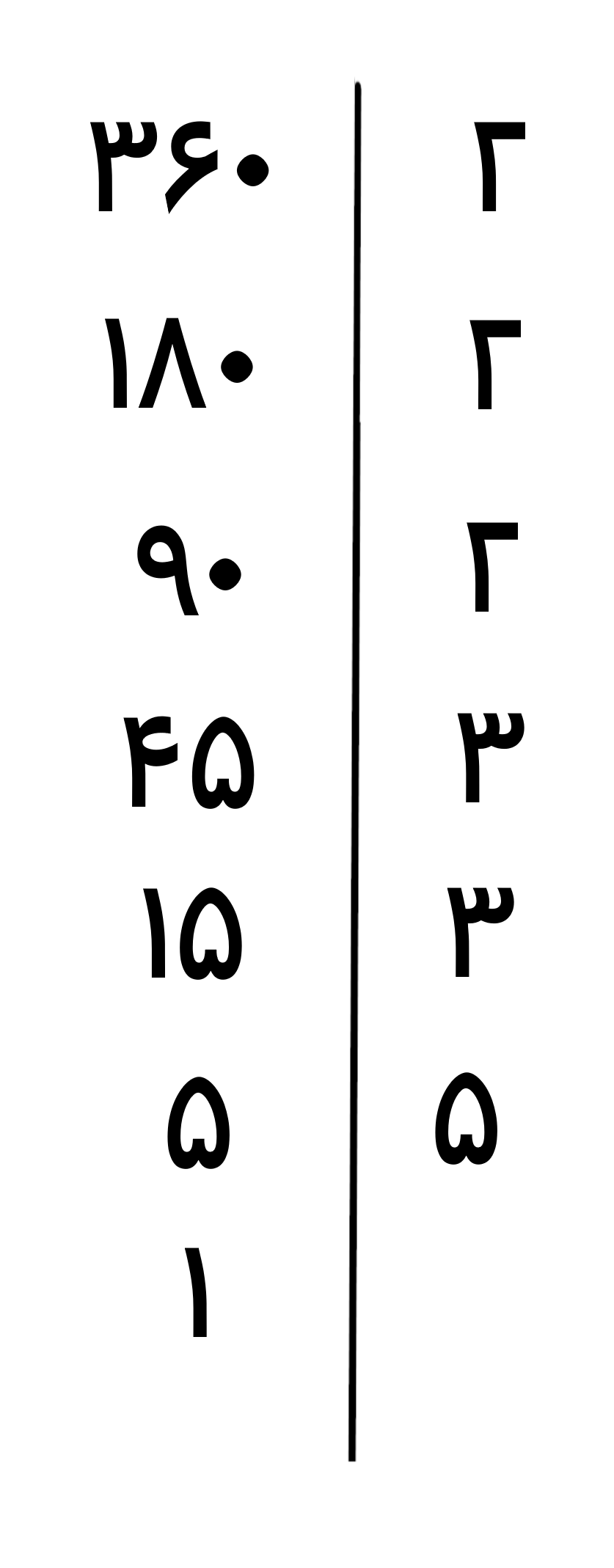
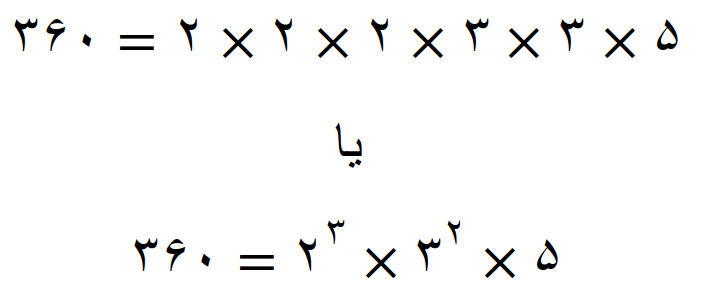
ما در تجزیه اعداد از روش های متفاوتی استفاده کردیم تا شما این موضوع را ببینید که فرقی ندارد که از چه شیوه ای عدد را به عامل های اول آن تجزیه می کنید(تا زمانی که در سوال از شما خواسته نشود به روش خاصی تجزیه کنید شما در انتخاب روش تجزیه عدد آزاد هستید، می توانید از همه روش ها استفاده کنید یا تنها یک روش را برای تجزیه این اعداد به کار ببرید؛ هر کدام که آسان تر هست و شما آن را بهتر یاد گرفتید).
کوچکترین مضرب مشترک مساوی است با، عامل های مشترک با توان بیشتر ضربدر عامل های غیر مشترک
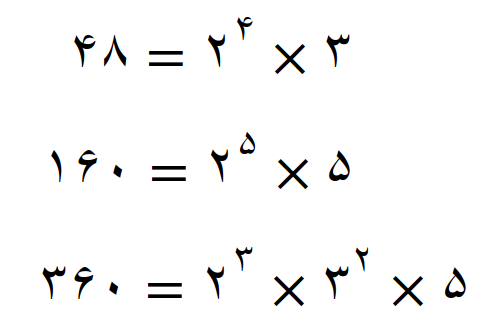
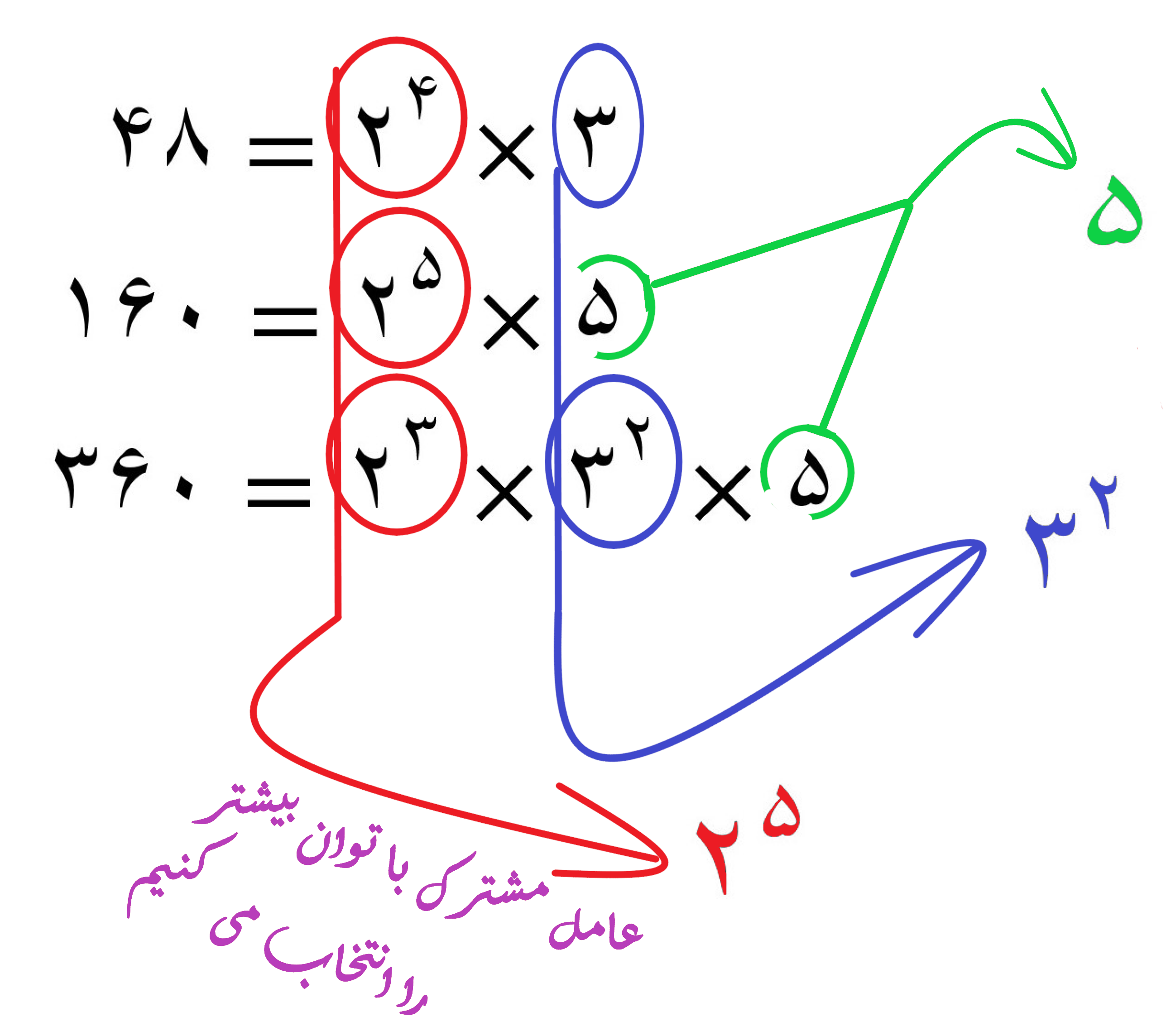
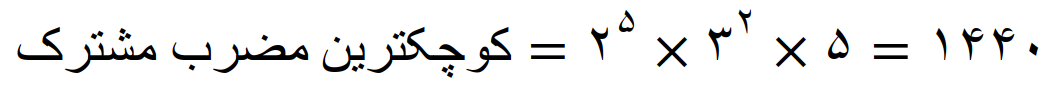
در نتیجه اولین مضرب مشترک این عددها، عدد 1440 می باشد پس داریم
99 مین مضرب مشترک سه عدد 48، 160 و 360 برابر است با
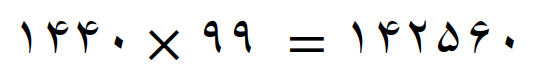
جواب بدست آمد
نکته 4
کوچکترین مضرب مشترک را با ک م م نمایش می دهند که اولین حروف کلمه های این عبارت هستند.
روش سوم
این روش تقریباً شبیه روش تجزیه ستونی می باشد؛ این روش را با یک مثال توضیح می دهیم.
می خواهیم کوچکترین مضرب مشترک سه عدد 48، 160 و 360 را با این شیوه بدست آوریم
ابتدا به تعداد اعدادی که می خواهیم کوچکترین مضرب مشترک آن ها را حساب کنیم خط عمودی می کشیم و عددها را مثل شکل زیر قرار می دهیم
چون اینجا می خواهیم کوچکترین مضرب مشترک سه عدد را پیدا کنیم پس سه تا خط عمودی می کشیم
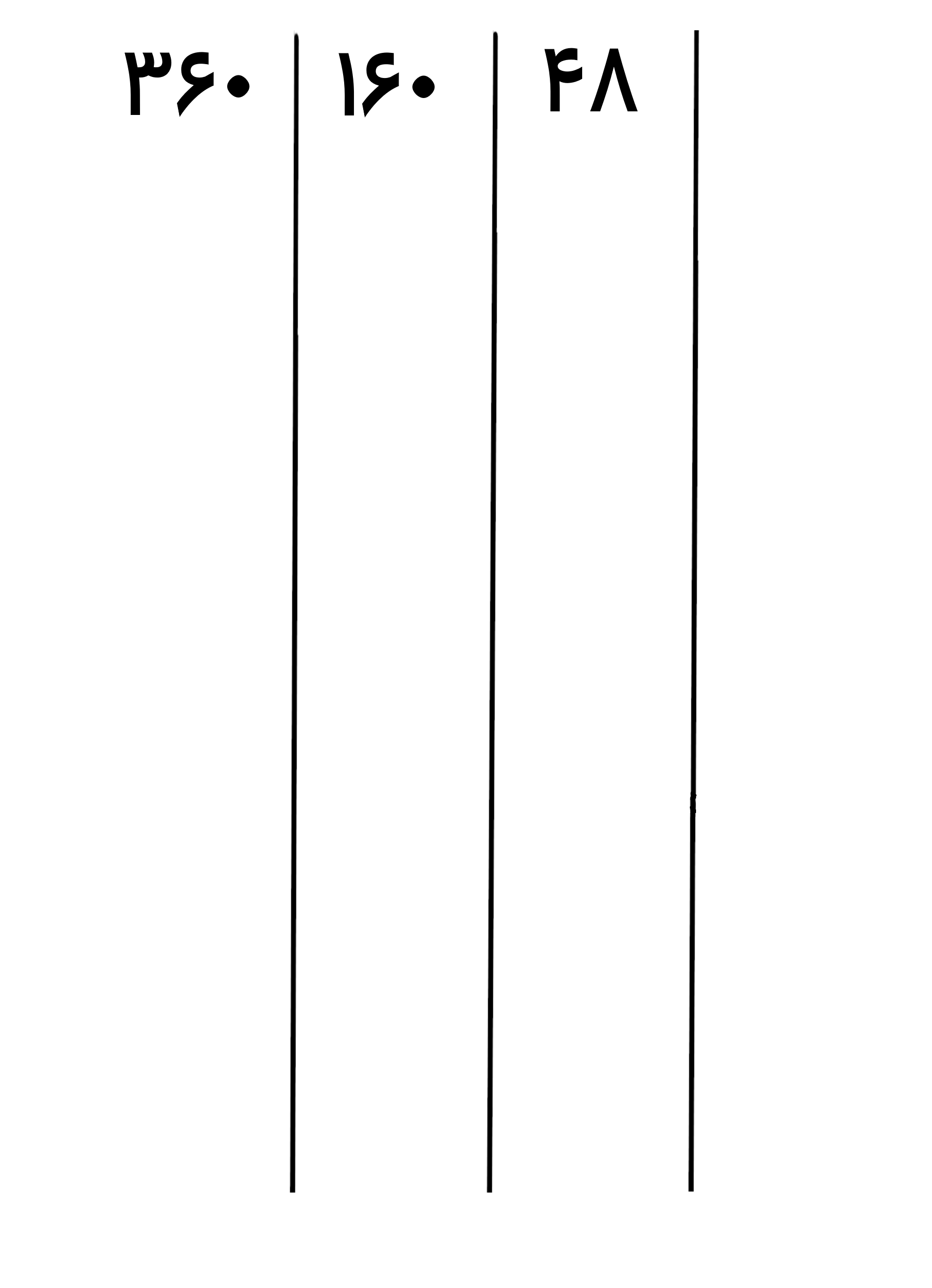
حالا بررسی می کنیم که این اعداد بر کدام عدد اول بخش پذیر هستند و از بین آن ها کوچکترین عدد اول را در سمت راست این جدول می نویسیم
هر سه این عددها بر عدد اول 2 بخش پذیر هستند پس عدد 2 را سمت راست جدول می نویسیم(میشه گفت، اولین ستون از سمت راست) و عددها را بر 2 تقسیم می کنیم و حاصل را زیر آن ها می نویسیم. به شکل زیر نگاه کنید
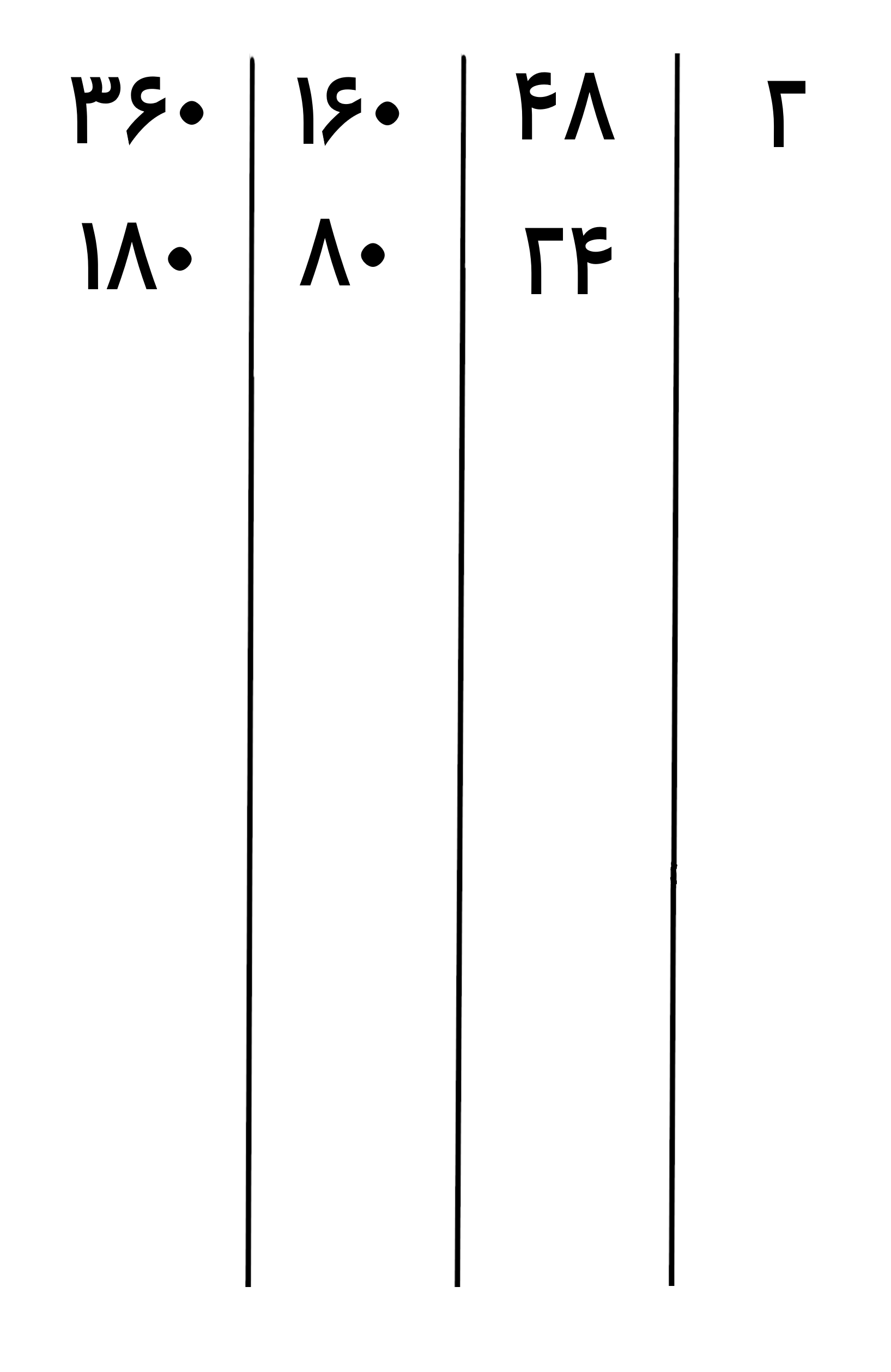
حالا بخش پذیری عدد های جدید(24، 80 و 180) را بر اعداد اول بررسی می کنیم و کوچکترین عدد اولی که آن ها بر آن بخشپذیر هستند را می نویسیم که مشخص است که این اعداد بر عدد اول 2 بخش پذیر هستند پس آن را سمت راست جدول می نویسیم و اعداد را بر 2 تقسیم کرده و حاصل را زیر آن ها می نویسیم
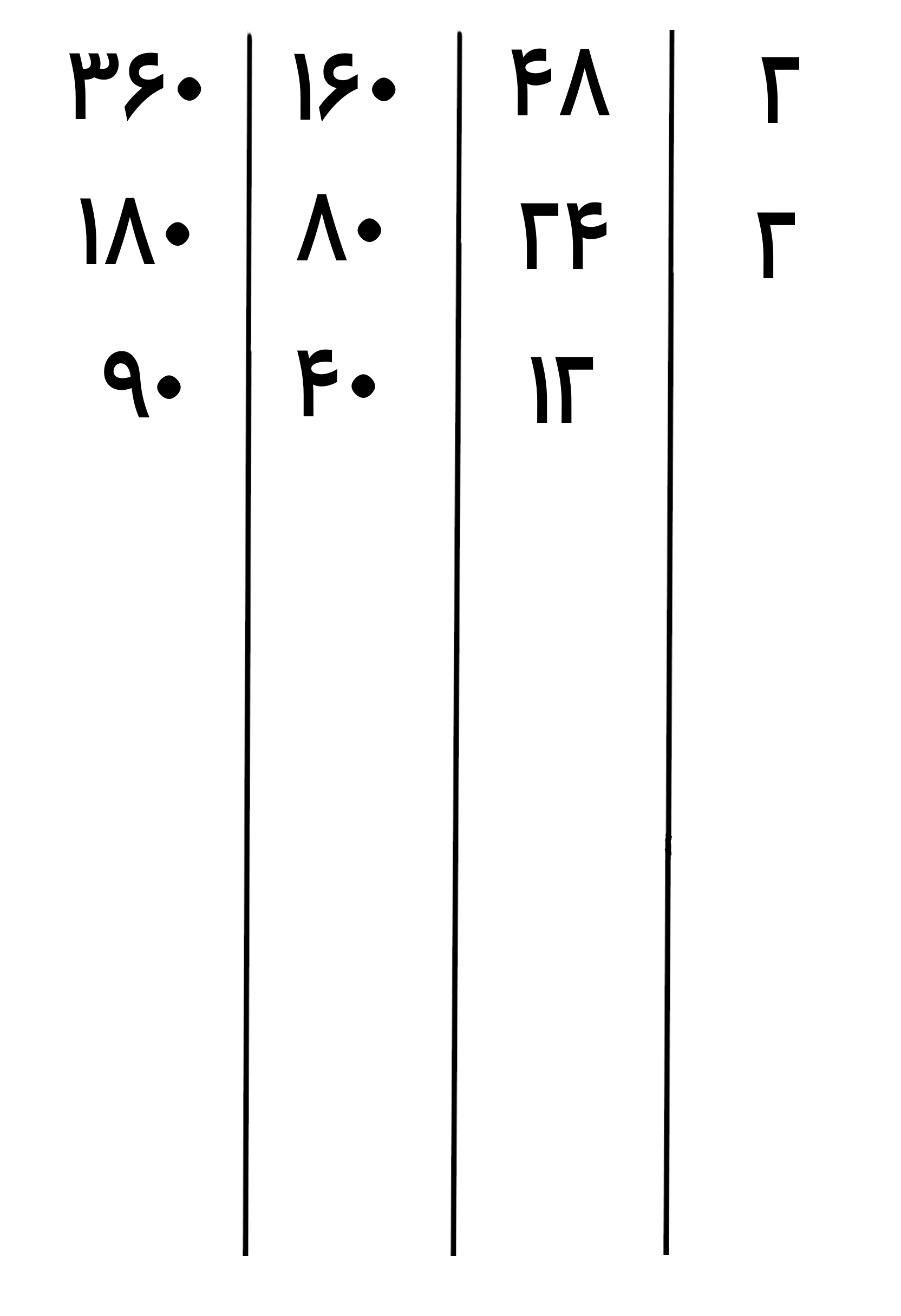
حالا بخش پذیری عدد های جدید(12، 40 و 90) را بر اعداد اول بررسی می کنیم و کوچکترین عدد اولی که آن ها بر آن بخشپذیر هستند را می نویسیم که مشخص است که این اعداد بر عدد اول 2 بخش پذیر هستند پس آن را سمت راست جدول می نویسیم و اعداد را بر 2 تقسیم کرده و حاصل را زیر آن ها می نویسیم
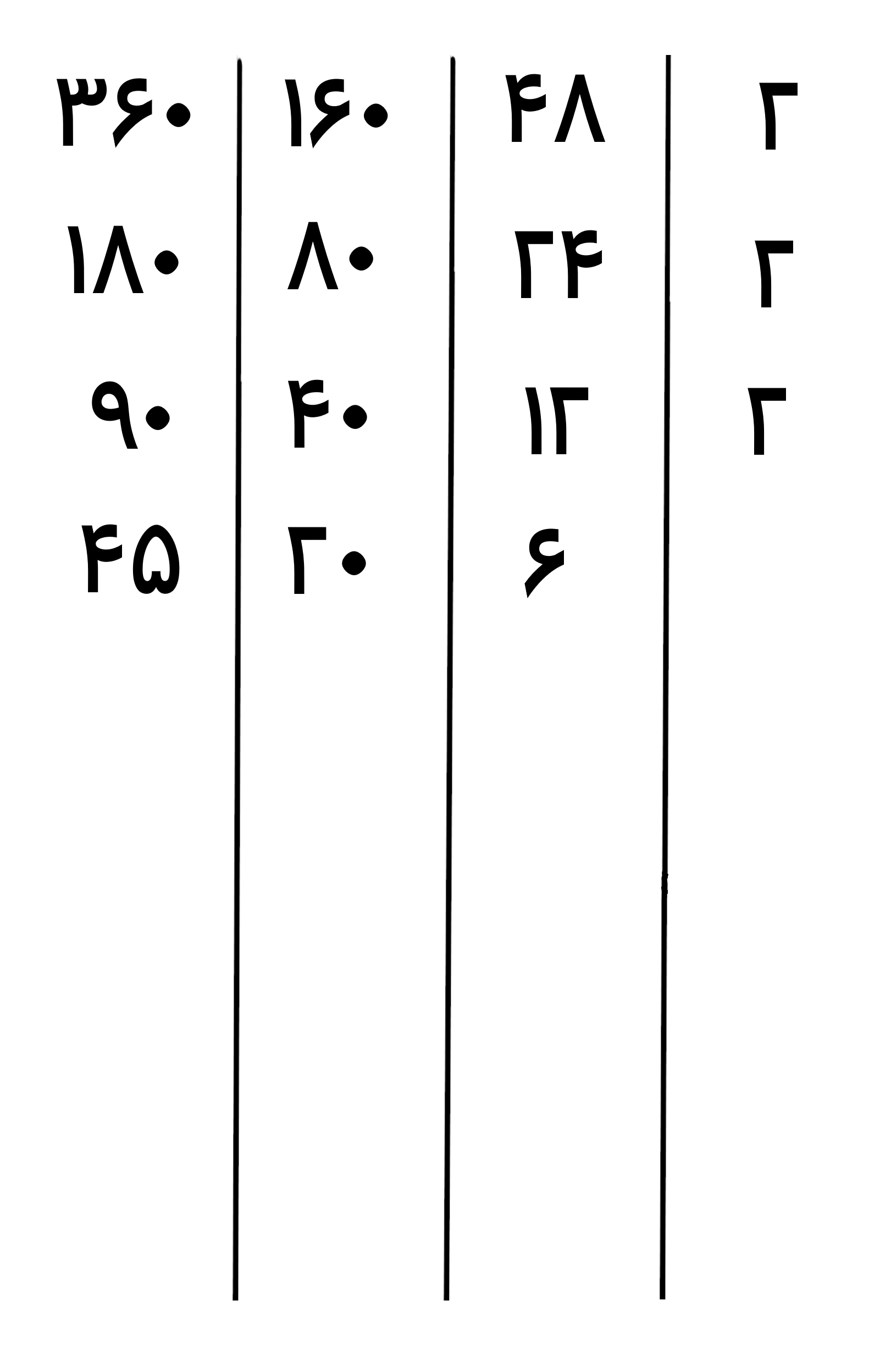
حالا بخش پذیری عدد های جدید(6، 20 و 45) را بر اعداد اول بررسی می کنیم و کوچکترین عدد اولی که آن ها بر آن بخشپذیر هستند را می نویسیم عدد 6 و 20 بر عدد اول 2 بخش پذیر هستند پس آن را سمت راست جدول می نویسیم و اعداد را بر 2 تقسیم کرده و حاصل را زیر آن ها می نویسیم(عدد 45 بر عدد اول 3 بخش پذیر است و ما از بین عددهای اول بدست آمده یعنی 2 و 3، کوچکترین عدد اول را در سمت راست جدول نوشتیم)
دقت کنید، چون عدد 45 بر 2 بخش پذیر نیست ما عدد 45 را بدون انجام تقسیم زیر آن می نویسیم
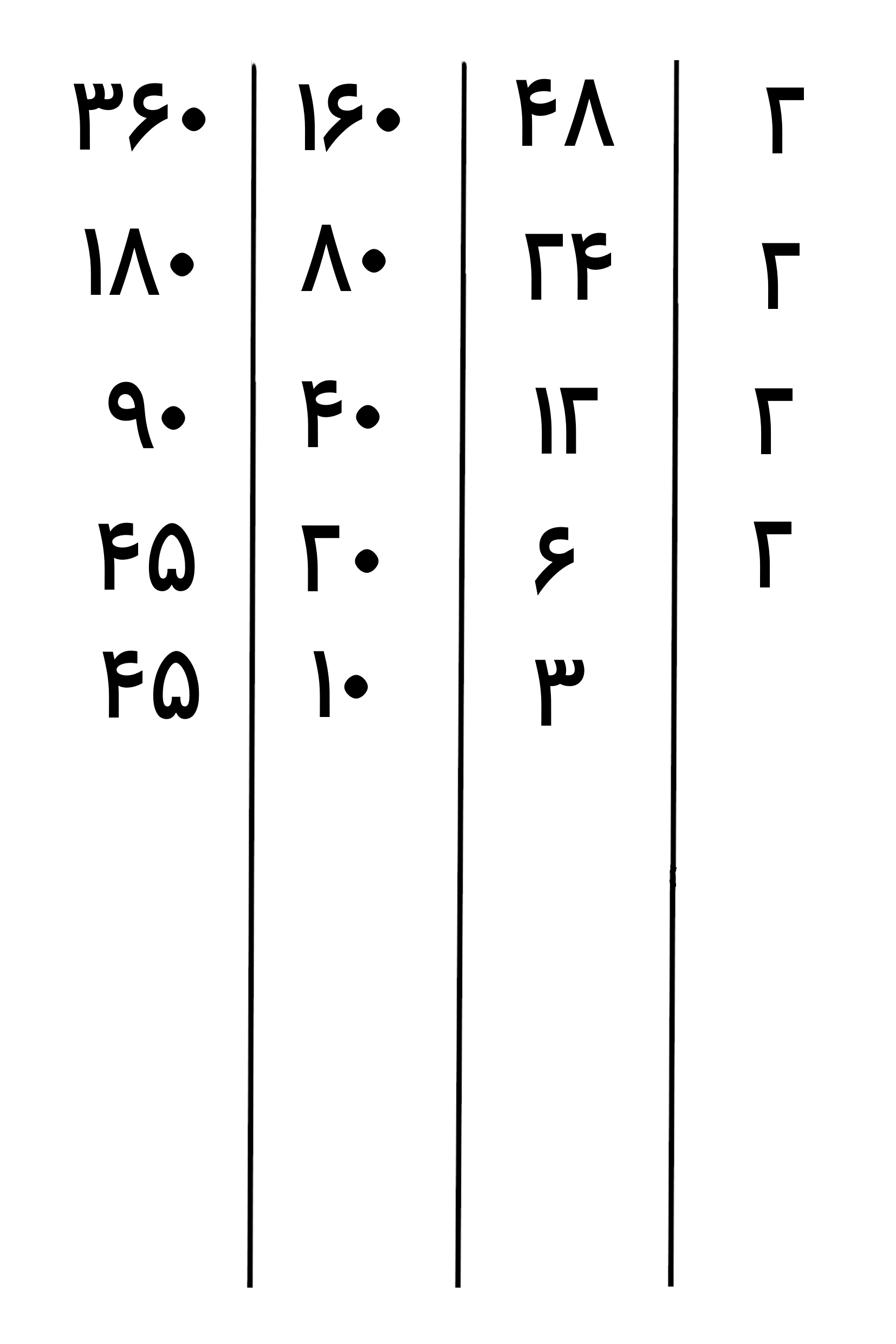
حالا بخش پذیری عدد های جدید(3، 10 و 45) را بر اعداد اول بررسی می کنیم و کوچکترین عدد اولی که آن ها بر آن بخشپذیر هستند را سمت راست جدول می نویسیم عدد 10 بر عدد اول 2 بخش پذیر هست پس آن را سمت راست جدول می نویسیم و اعدادی را که بر 2 قابل تقسیم هستند را بر 2 تقسیم می کنیم و حاصل را زیر آن ها می نویسیم(عددهای 3 و 45 بر عدد اول 3 بخش پذیر هستند و ما از بین عددهای اول بدست آمده یعنی 2 و 3، کوچکترین عدد اول را در سمت راست جدول نوشتیم)
دقت کنید، چون عدد های 3 و 45 بر 2 بخش پذیر نیستند ما این عددها را بدون انجام تقسیم زیر آن می نویسیم
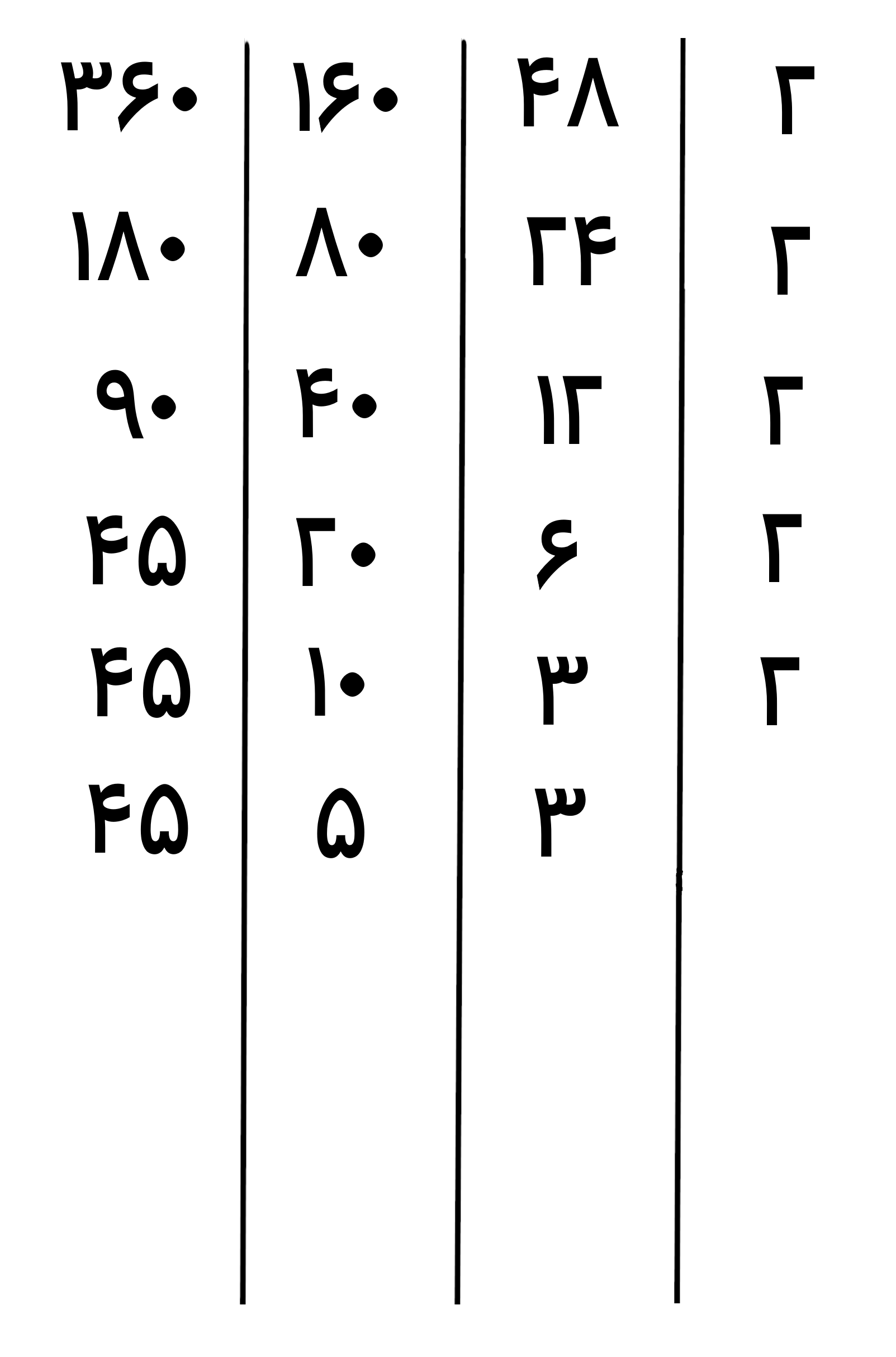
حالا بخش پذیری عدد های جدید(3، 5 و 45) را بر اعداد اول بررسی می کنیم و کوچکترین عدد اولی که آن ها بر آن بخش پذیر هستند را سمت راست جدول می نویسیم عددهای 3 و 45 بر عدد اول 3 بخش پذیر هستند پس آن را سمت راست جدول می نویسیم و اعدادی را که بر 3 قابل تقسیم هستند را بر 3 تقسیم می کنیم و حاصل را زیر آن ها می نویسیم(عدد 5 بر عدد اول 5 بخش پذیر هست و ما از بین عددهای اول بدست آمده یعنی 3 و 5، کوچکترین عدد اول را در سمت راست جدول نوشتیم)
دقت کنید، چون عدد 5 بر 3 بخش پذیر نیست ما این عدد را بدون انجام تقسیم زیر آن می نویسیم
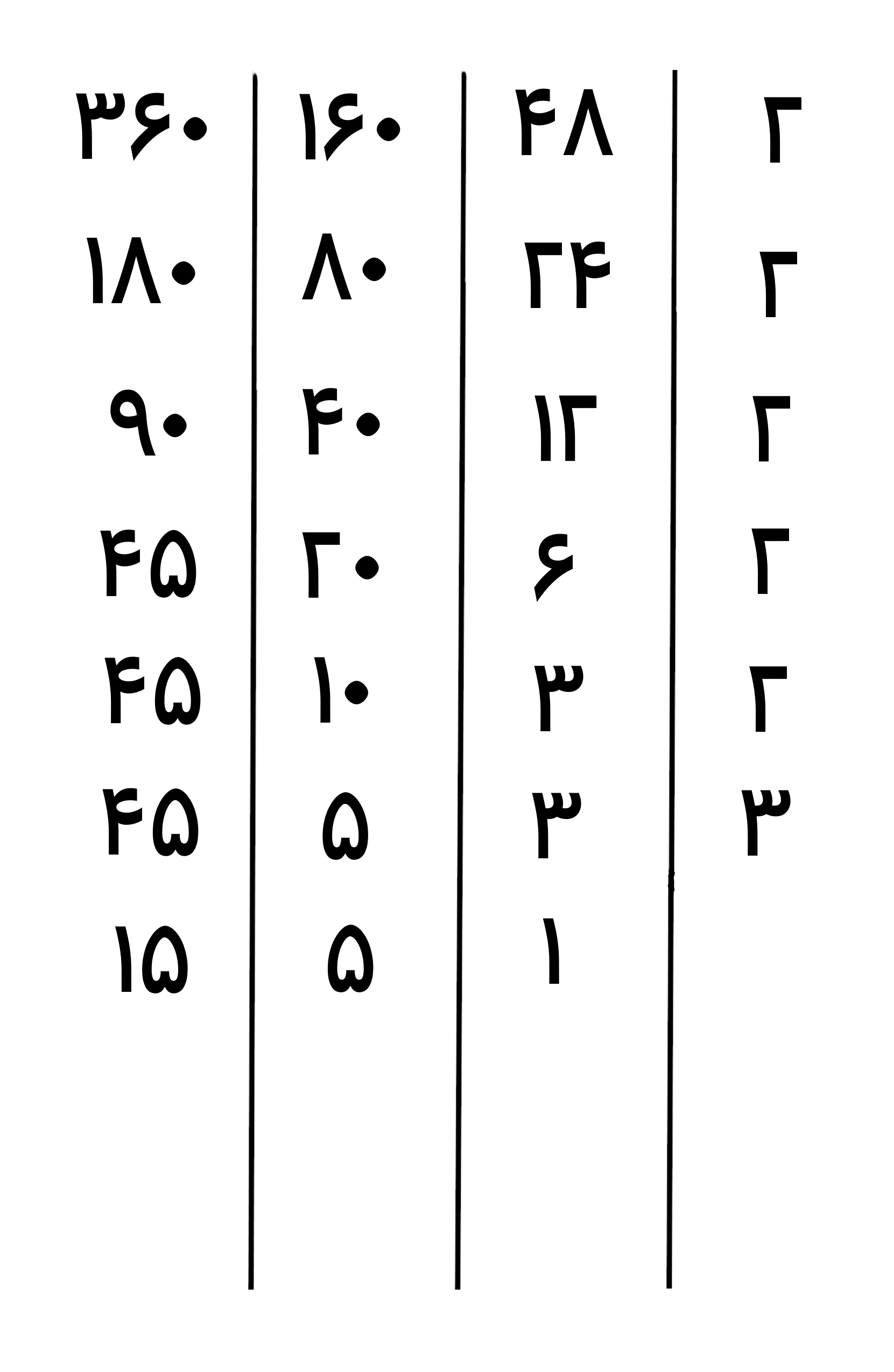
حالا بخش پذیری عدد های جدید(5 و 15) را بر اعداد اول بررسی می کنیم و کوچکترین عدد اولی که آن ها بر آن بخش پذیر هستند را سمت راست جدول می نویسیم
عدد 1 در ستون دوم به ما نشان می دهد که تجزیه عدد 48 به پایان رسیده، پس دیگر در بررسی بخش پذیری بر اعداد اول با این ستون کاری نداریم و عدد 1 را در ستون دوم تا رسیدن سایر ستون ها به عدد 1 تکرار می کنیم
عدد 15 بر عدد اول 3 بخش پذیر است پس آن را سمت راست جدول می نویسیم و اعدادی را که بر 3 قابل تقسیم هستند را بر 3 تقسیم می کنیم و حاصل را زیر آن ها می نویسیم(عدد 5 بر عدد اول 5 بخش پذیر هست و ما از بین عددهای اول بدست آمده یعنی 3 و 5، کوچکترین عدد اول را در سمت راست جدول نوشتیم)
دقت کنید، چون عدد 5 بر 3 بخش پذیر نیست ما این عدد را بدون انجام تقسیم زیر آن می نویسیم
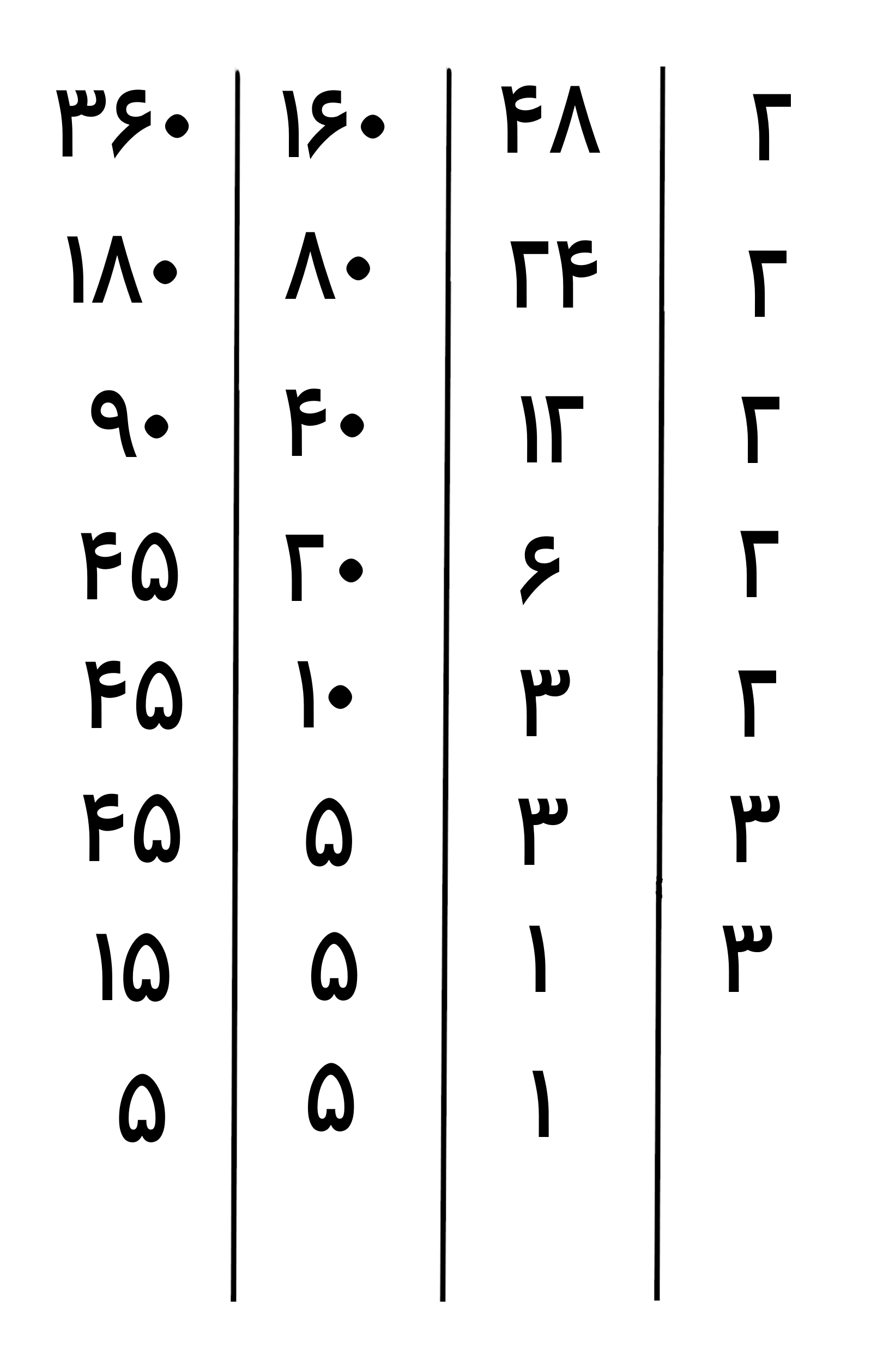
در این مرحله تنها عدد 5 را داریم که بر 5 بخش پذیر است پس آن را سمت راست جدول می نویسیم و اعدادی را که بر 5 قابل تقسیم هستند را بر 5 تقسیم می کنیم و حاصل را زیر آن ها می نویسیم
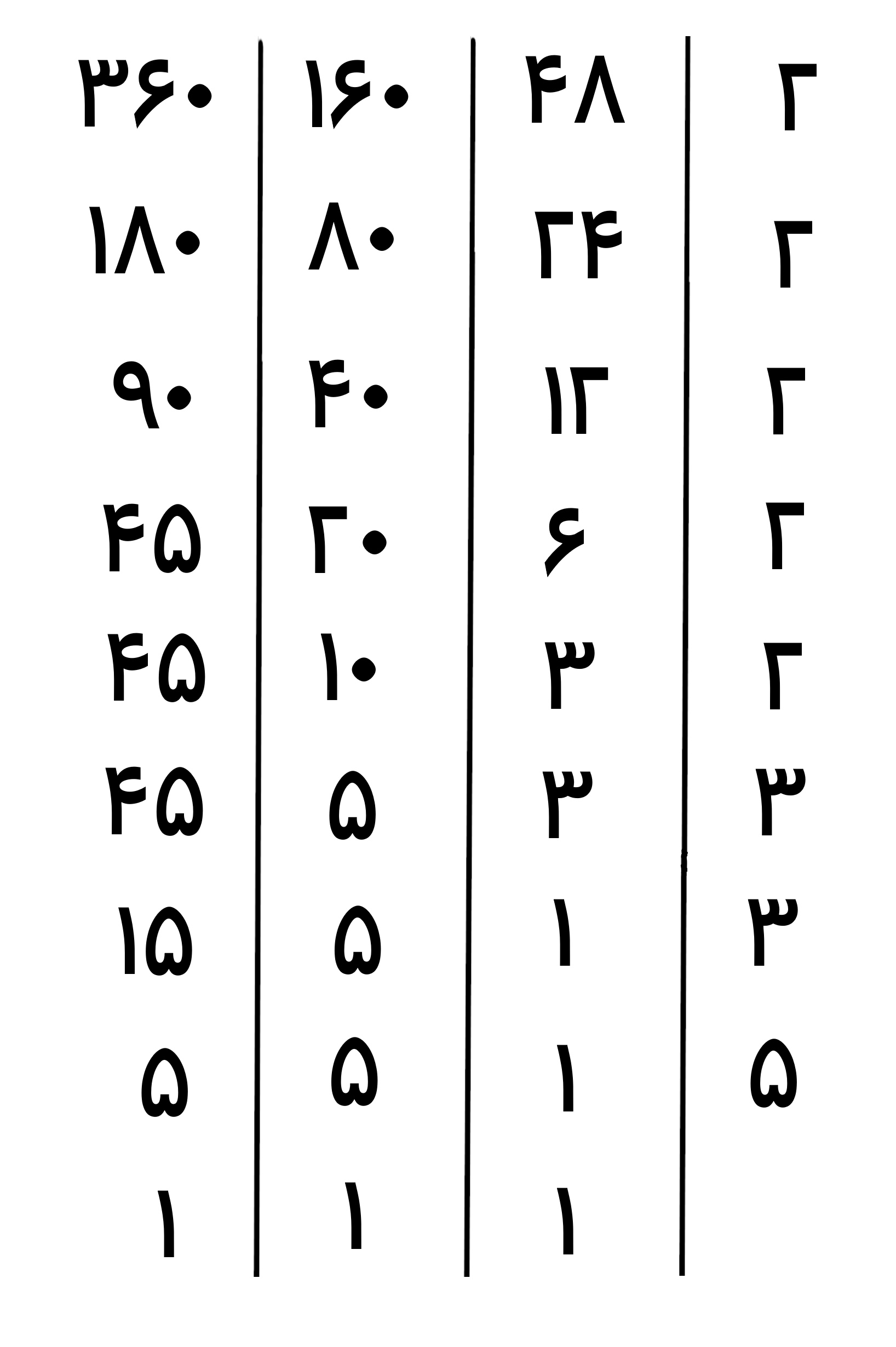
مشاهده می کنیم که در تجزیه عددها به عدد 1 رسیدیم پس کار تجزیه پایان یافت
حالا نوبت نوشتن کوچکترین مضرب مشترک این عدد ها است
ک م م سه عدد 48، 160 و 360 برابر است با حاصلضرب عددهای اولی که در ستون اول جدول نوشته شده(از سمت راست)؛ یعنی
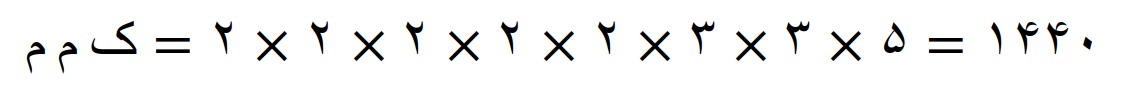
یا
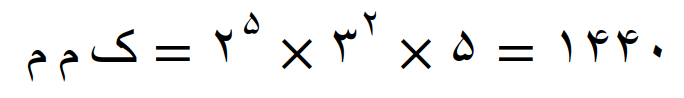
مثال 16
ک م م دو عدد 90 و 252 را بیابید
جواب: دو خط عمودی می کشیم(چون دو عدد داریم) و اعداد را در آن قرار می دهیم
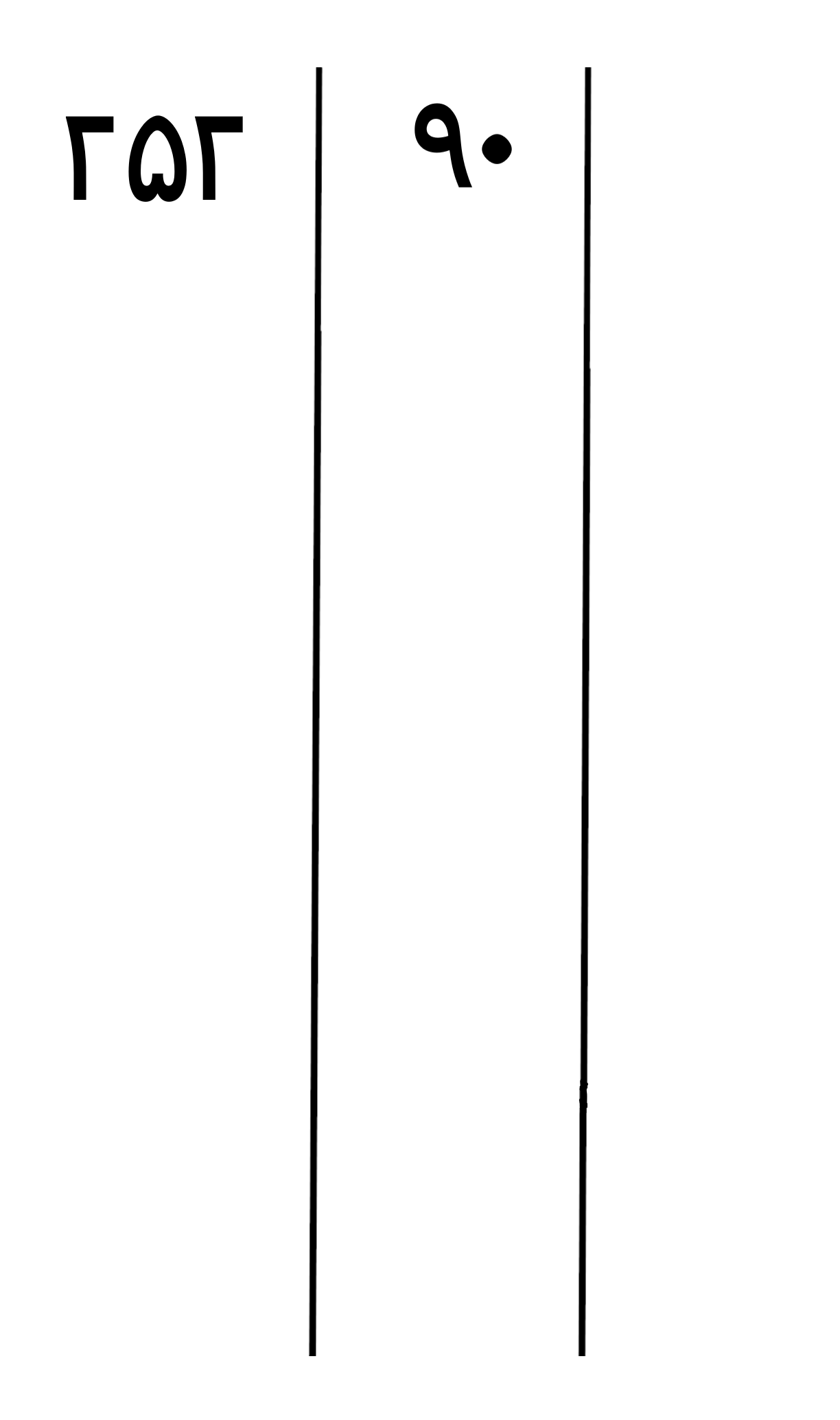
عدد 90 و عدد 252 هر دو بر عدد اول 2 بخش پذیر هستند پس عدد اول 2 را در ستون اول از سمت راست می نویسیم و بعد اعداد را بر 2 تقسیم می کنیم
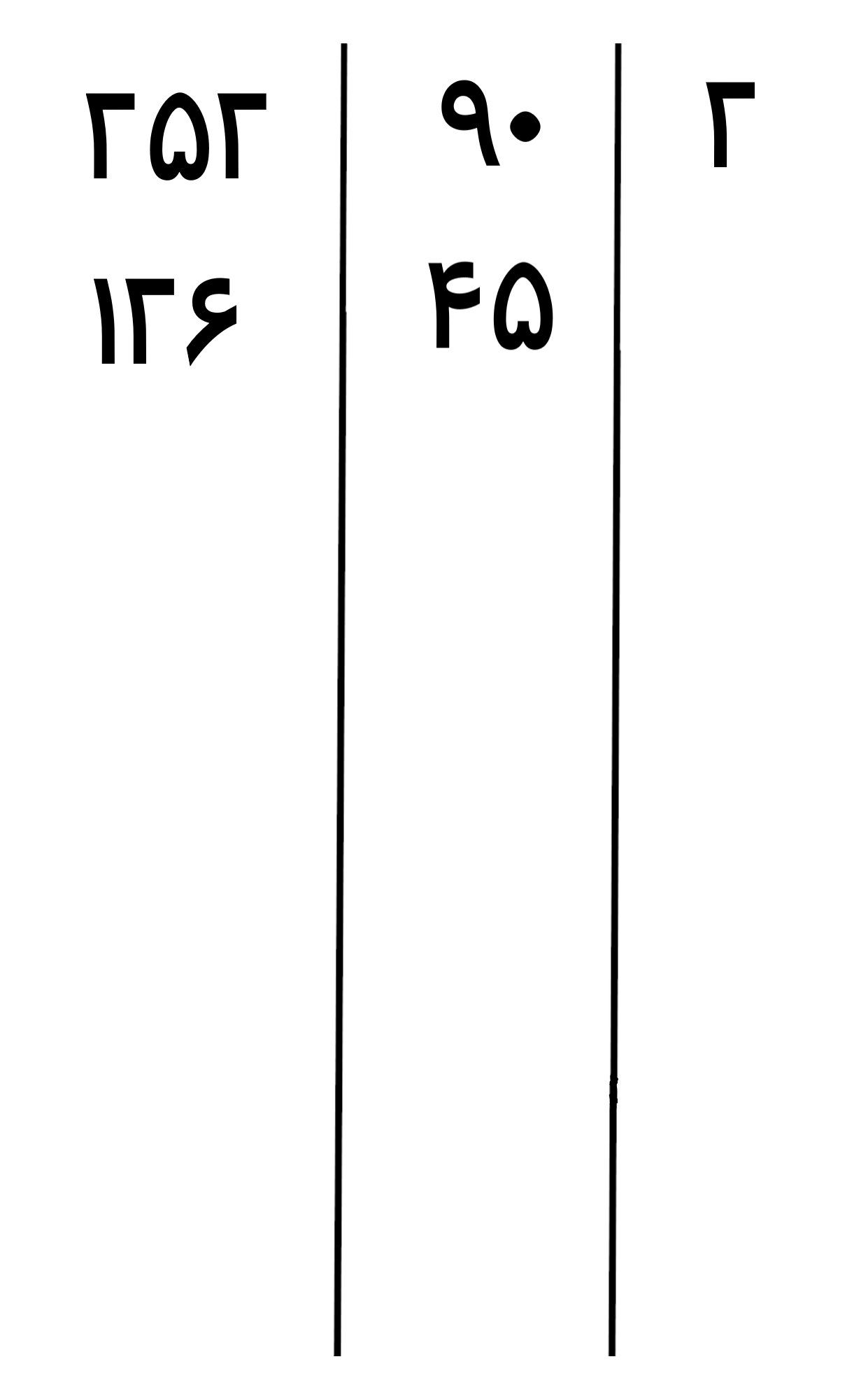
عدد 126 بر 2 بخش پذیر است و عدد 45 بر 3، پس عدد اول 2 را در ستون اول از سمت راست می نویسیم و بعد اعداد را بر 2 تقسیم می کنیم
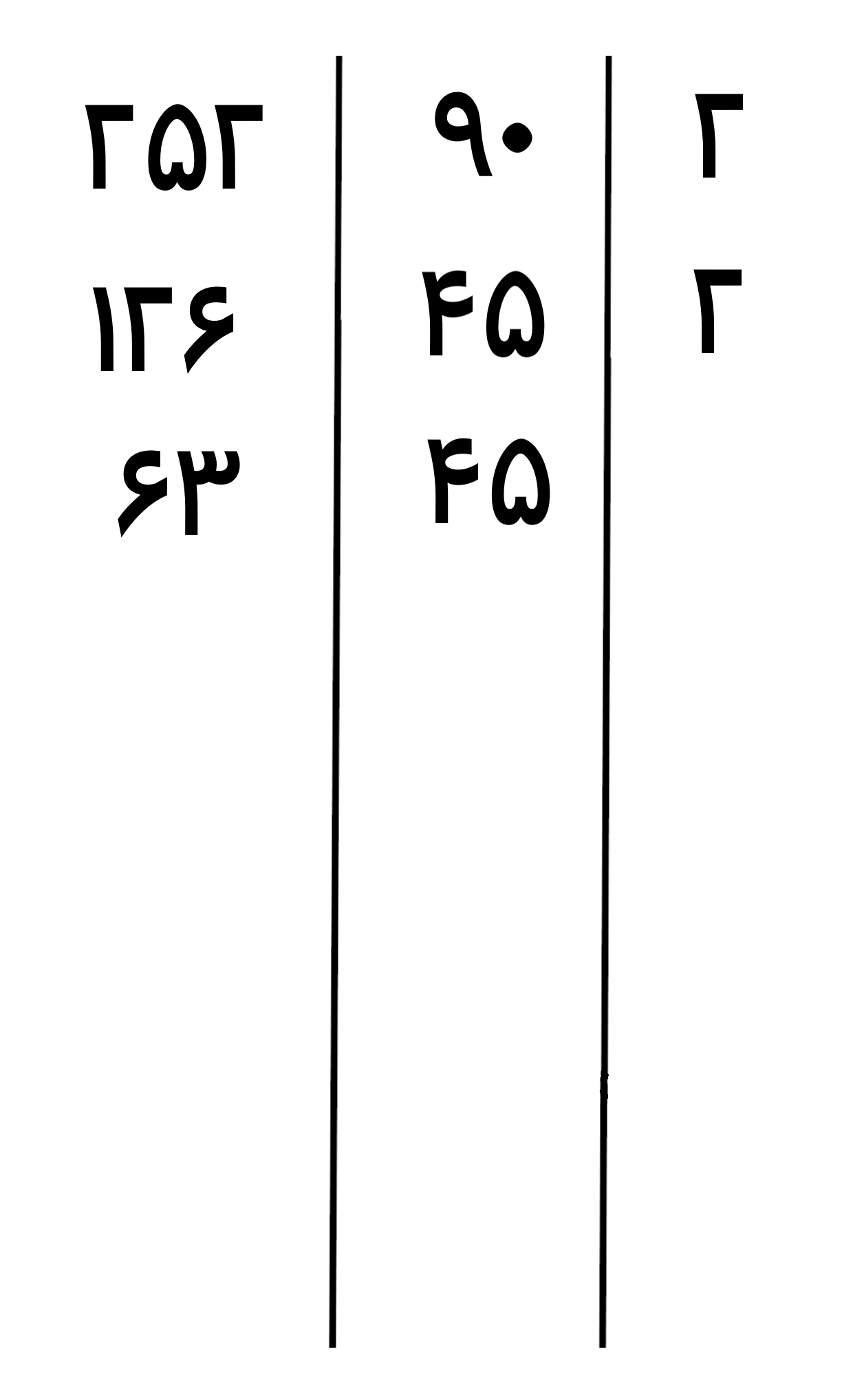
عدد 45 و عدد 63 هر دو بر 3 بخشپذیر هستند، پس عدد اول 3 را در ستون اول از سمت راست می نویسیم و بعد اعداد را بر عدد اول 3 تقسیم می کنیم
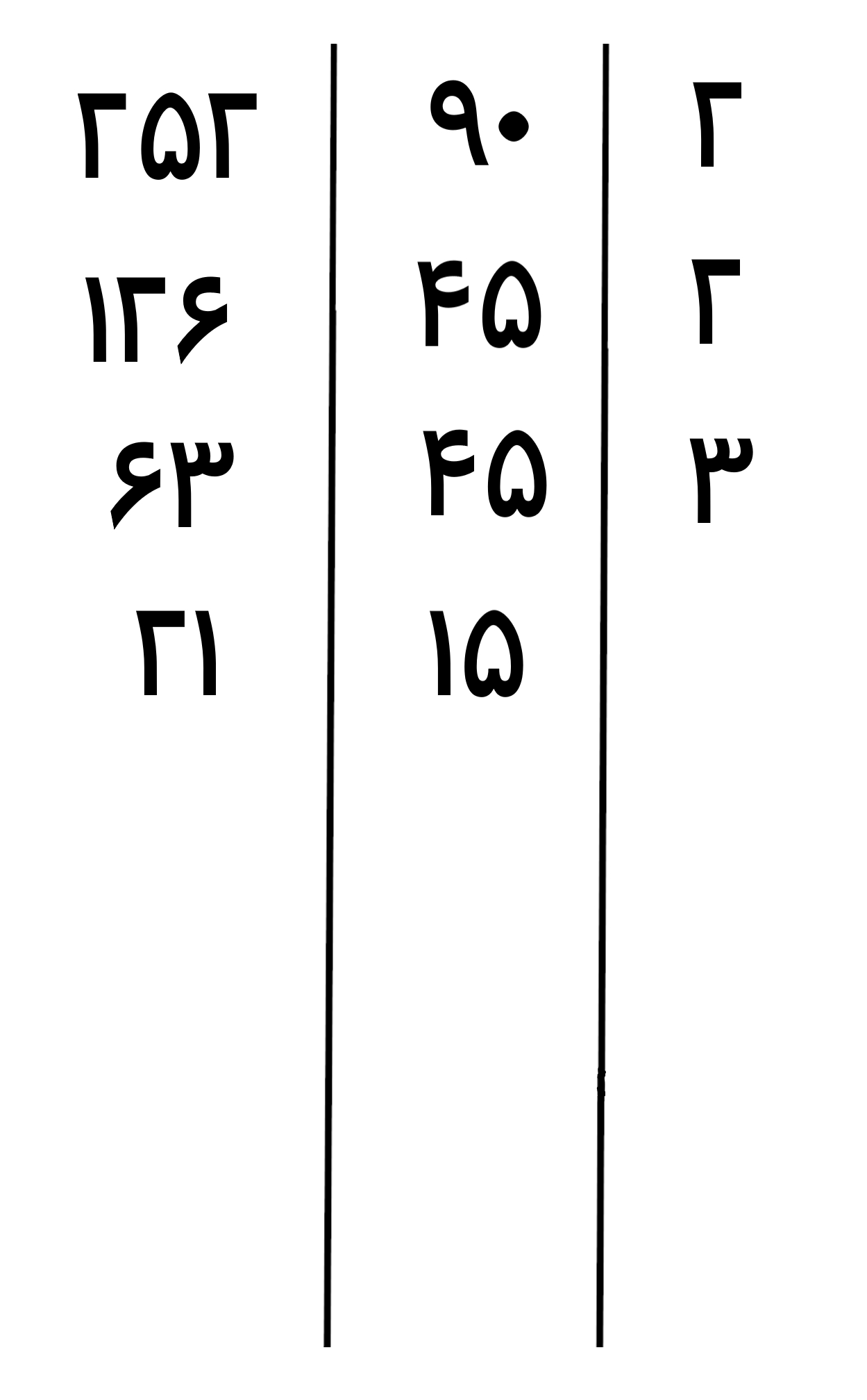
عدد 15 و عدد 21 هر دو بر 3 بخشپذیر هستند، پس عدد اول 3 را در ستون اول از سمت راست می نویسیم و بعد اعداد را بر عدد اول 3 تقسیم می کنیم
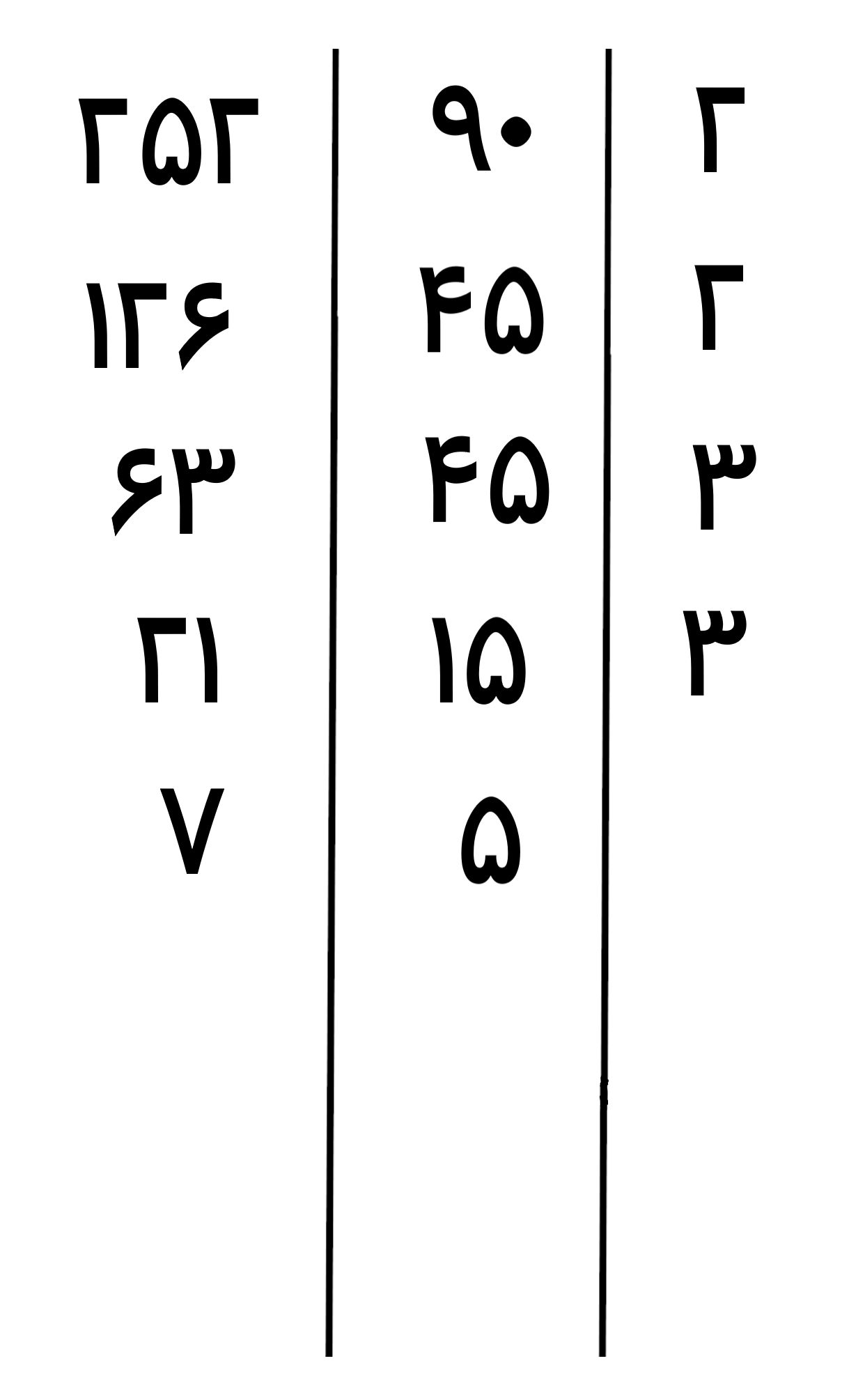
عدد 5 بر عدد اول 5 بخش پذیر هست و عدد 7 بر عدد اول 7، پس عدد اول 5 را در ستون اول از سمت راست می نویسیم و بعد اعداد را بر عدد اول 5 تقسیم می کنیم
عدد 7 بر 5 قابل تقسیم نیست(باقیمانده صفر و حاصل تقسیم عدد صحیح نمی شود) پس عدد 7 را بدون انجام تقسیم می نویسیم
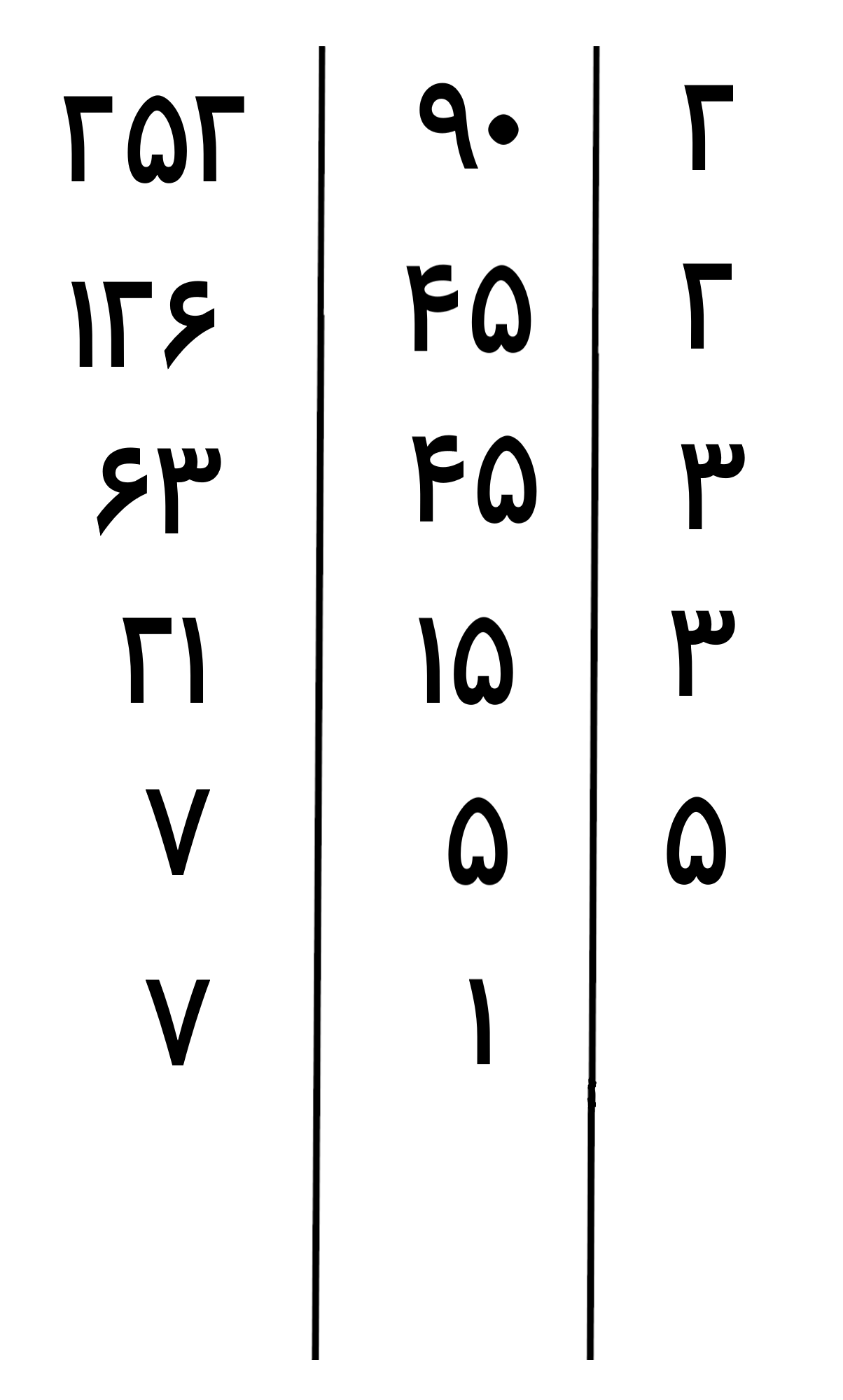
عدد 1 نشان می دهد که تجزیه عدد 90 به پایان رسیده؛ البته دقت کنید که این به معنی آن نیست که اعداد اول موجود در ستون اول از سمت راست، تجزیه عدد 90 هستند(حاصلضرب اعداد اول بدست آمده 180 می شود نه 90، چون ما عدد اول 2 را بار دوم برای تجزیه عدد 252 در ستون اول نوشتیم که ارتباطی به تجزیه عدد 90 نداشته)
عدد 7 بر عدد اول 7 بخش پذیر هست، پس عدد اول 7 را در ستون اول از سمت راست می نویسیم و بعد اعداد را بر عدد اول 7 تقسیم می کنیم
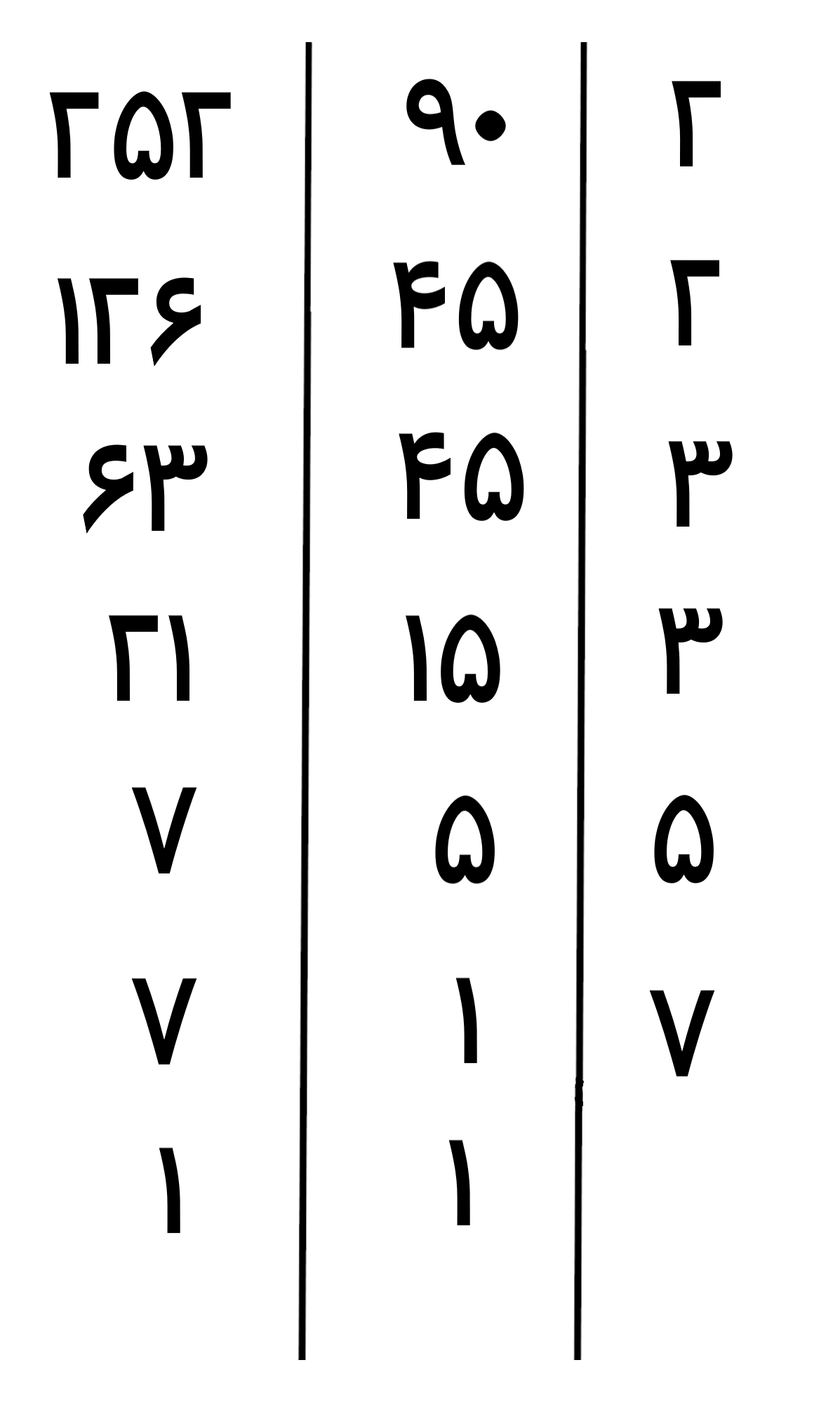
می بینیم که به عدد 1 رسیدیم پس کار تجزیه این اعداد به پایان رسید
کوچکترین مضرب مشترک(ک م م) مساوی است با حاصل ضرب اعداد اولی که در اولین ستون سمت راست این جدول وجود دارند
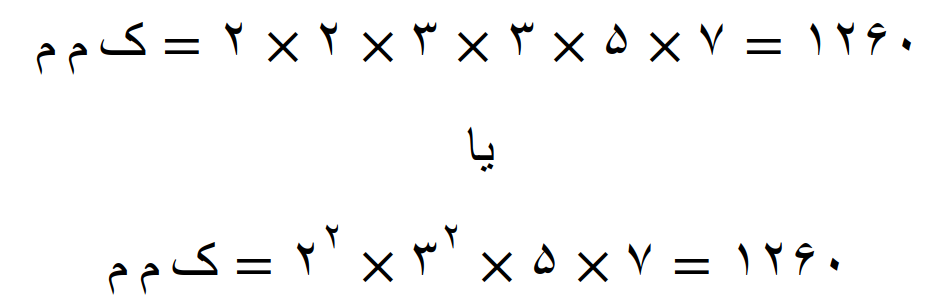
مثال 17
کوچکترین مضرب مشترک(ک م م) شش عدد 25، 40، 49، 80، 90 و 125 را بنویسید
جواب:

ک م م برابر است با حاصل ضرب اعداد اولی که در اولین ستون سمت راست این جدول نوشته شده اند
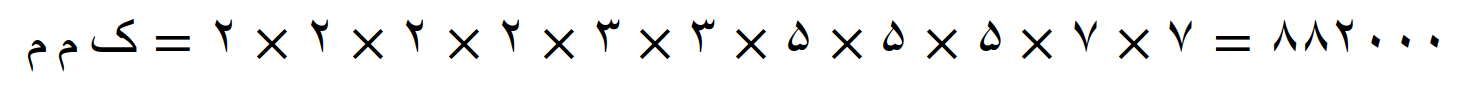
یا
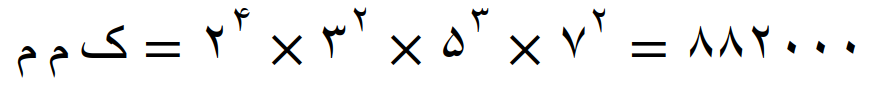
در نتیجه کوچکترین مضرب مشترک این شش عدد مساوی است با
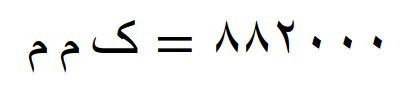
لینک کوتاه این مطلب: https://tadris.dabidi.ir/lcmn
مضارب اعداد و محاسبه کوچکترین مضرب مشترک (ک م م)

