تعریف و تشخیص اعداد اول به همراه لیست 1000 عدد اول نخست | دانلود فهرست 100008 عدد اول نخست | عدد اول، عددی است که فقط دو شمارنده داشته باشد
فهرست محتوا
- تعریف عدد اول:
- بررسی عدد اول بودن یا نبودن اعداد
- آیا می توان الگویی برای اول نبودن یک عدد پیدا کرد؟!
- تشخیص عدد اول بودن یا اول نبودن یک عدد
- فهرست ۱۰۰۰ عدد اول
- دانلود لیست 100008 عدد اول نخست
تعریف عدد اول:
اعداد اول به اعداد طبیعی گفته می شوند که تنها به 1 و خود آن عدد دقیقاً قابل تقسیم یا بخش پذیر هستند یعنی مقسوم علیه های عدد اول، یک و خودش است(اعداد اول، اعدادی هستند که فقط دو شمارنده داشته باشند).
تعریف بخش پذیری: اگر حاصل تقسیم یک عدد بر عدد دیگر، عددی صحیح باشد و باقیمانده تقسیم برابر با صفر شود اصطلاحاً می گوییم که عدد اولی بر عدد دومی بخش پذیر است.
بررسی عدد اول بودن یا نبودن اعداد
مجموعه اعداد طبیعی را با N نمایش می دهند که حرف اول کلمه Natural است
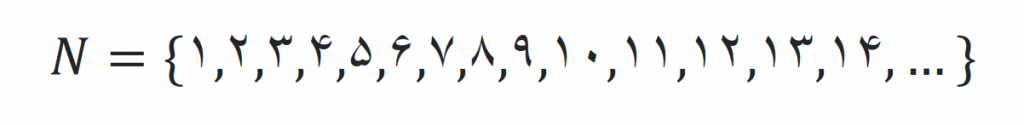
نکته مهم: این را به خاطر داشته باشید که عدد 1 عدد اول نیست(چرا؟).
بنابراین با توجه به مجموعه اعداد طبیعی و اینکه 1 عدد اول نیست، مجموعه زیر را داریم که باید اول بودن یا نبودن اعداد موجود در آن را بررسی کنیم
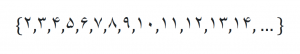
نکته: تمام اعداد طبیعی بر 1 بخش پذیر هستند و عدد 1 مقسوم علیه همه اعداد طبیعی است.
بررسی عدد اول بودن یا نبودن اعداد مجموعه
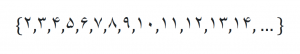
عدد 2 بر 1 و 2 بخش پذیر است پس نتیجه 1 و خود عدد است بنابراین 2 عددی اول است(عدد 1 و 2 مقسوم علیه 2 می باشند)
عدد 3 بر 1 و 3 بخش پذیر است پس نتیجه 1 و خود عدد است بنابراین 3 عددی اول است
عدد 4 بر 1 و 2 و 4 بخش پذیر است که در نتیجه بر عددی غیر از 1 و خودش بخش پذیر است پس 4 عددی اول نیست(عدد 1 و 2 و 4 مقسوم علیه 4 می باشند)
عدد 5 بر 1 و 5 بخش پذیر است پس نتیجه 1 و خود عدد است بنابراین 5 عددی اول است
عدد 6 بر 1 و 2 و3 و 6 بخش پذیر است که در نتیجه بر اعدادی غیر از 1 و خودش بخش پذیر است پس 6 عددی اول نیست
عدد 7 بر 1 و 7 بخش پذیر است پس نتیجه 1 و خود عدد است بنابراین 7 عددی اول است
عدد 8 بر 1 و 2 و 4 و 8 بخش پذیر است که در نتیجه بر اعدادی غیر از 1 و خودش بخش پذیر است پس 8 عددی اول نیست
عدد 9 بر 1 و 3 و 9 بخش پذیر است که در نتیجه بر عددی غیر از 1 و خودش بخش پذیر است پس 9 عددی اول نیست
عدد 10 بر 1 و 2 و 5 و 10 بخش پذیر است که در نتیجه بر اعدادی غیر از 1 و خودش بخش پذیر است پس 10 عددی اول نیست
عدد 11 بر 1 و 11 بخش پذیر است پس نتیجه 1 و خود عدد است بنابراین 11 عددی اول است
عدد 12 بر 1 و 2 و 3 و 4 و 6 و 12 بخش پذیر است که در نتیجه بر اعدادی غیر از 1 و خودش بخش پذیر است پس 12 عددی اول نیست
عدد 13 بر 1 و 13 بخش پذیر است پس نتیجه 1 و خود عدد است بنابراین 13 عددی اول است
عدد 14 بر 1 و 2 و 7 و 14 بخش پذیر است که در نتیجه بر اعدادی غیر از 1 و خودش بخش پذیر است پس 14 عددی اول نیست
عدد 15 بر 1 و 3 و 5 و 15 بخش پذیر است که در نتیجه بر اعدادی غیر از 1 و خودش بخش پذیر است پس 15 عددی اول نیست
عدد 16 بر 1 و 2 و 4 و 8 و 16 بخش پذیر است که در نتیجه بر اعدادی غیر از 1 و خودش بخش پذیر است پس 16 عددی اول نیست
عدد 17 بر 1 و 17 بخش پذیر است پس نتیجه 1 و خود عدد است بنابراین 17 عددی اول است
عدد 18 بر 1 و 2 و 3 و 6 و 9 و 18 بخش پذیر است که در نتیجه بر اعدادی غیر از 1 و خودش بخش پذیر است پس 18 عددی اول نیست
عدد 19 بر 1 و 19 بخش پذیر است پس نتیجه 1 و خود عدد است بنابراین 19 عددی اول است
عدد 20 بر 1 و 2 و 4 و 5 و 10 و 20 بخش پذیر است که در نتیجه بر اعدادی غیر از 1 و خودش بخش پذیر است پس 20 عددی اول نیست
همان طور که مشاهده کردید اعدادی که بر عددی غیر از 1 و خود آن عدد بخش پذیر هستند عدد اول نمی باشند؛ پس برای فهمیدن این که عددی اول نیست تنها کافی است یک عددی غیر از عدد 1 و خودش پیدا کنیم که بر آن بخش پذیر باشد.
عدد 21 بر 3 بخش پذیر است پس 21 عددی اول نیست(عدد 21 بر 1 و 3 و 7 و 21 بخش پذیر است ولی این اعداد را ننوشتیم چون همان طور که گفتیم این که به عددی غیر از 1 و خودش یعنی بر 3 بخش پذیر است کافیست تا ما متوجه شویم که این عدد، عددی اول نیست)
عدد 22 بر 2 بخش پذیر است پس 22 عددی اول نیست
عدد 23 تنها بر 1 و 23 بخش پذیر است پس 23 عددی اول است
عدد 24 بر 2 بخش پذیر است پس 24 عددی اول نیست
عدد 25 بر 5 بخش پذیر است پس 25 عددی اول نیست
عدد 26 بر 2 بخش پذیر است پس 26 عددی اول نیست
عدد 27 بر 3 بخش پذیر است پس 27 عددی اول نیست
عدد 28 بر 2 بخش پذیر است پس 28 عددی اول نیست
عدد 29 تنها بر 1 و 29 بخش پذیر است پس 29 عددی اول است
عدد 30 بر 2 بخش پذیر است پس 30 عددی اول نیست
عدد 31 تنها بر 1 و 31 بخش پذیر است پس 31 عددی اول است
به نتایج بالا نگاه کنید
آیا می توان الگویی برای اول نبودن یک عدد پیدا کرد؟!
22، 24، 26، 28، 30 بر 2 بخش پذیر هستند همین طور اعداد 20، 18، 16، 14، 12، 10، 8، … بر 2 بخش پذیر هستند.
همان طور که نتایج نشان می دهد این اعداد اول نیستند آیا این نتیجه همیشه برقرار است؟! یعنی هر عددی که بر 2 بخش پذیر باشد عددی اول نیست!
دوباره به مجموعه نگاه کنید
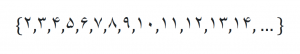
اعدادی که بر 2 بخش پذیر هستند را می نویسیم
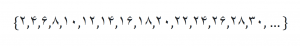
در واقع این اعداد مضرب 2 هستند
همان طور که مشخص است این مجموعه، مجموعه اعداد زوج است
حالا بر می گردیم به سوال قبل، اینکه “هر عددی که بر 2 بخش پذیر باشد عددی اول نیست!” را به صورت “هر عددی که زوج باشد عددی اول نیست!” می نویسیم؛ آیا این گزاره درست است؟!
خیر؛ این گزاره همواره برقرار نیست چون عدد زوج 2 بر 2 بخش پذیر می باشد ولی 2 عددی اول است
نکته: تنها عدد زوجی که عدد اول است عدد 2 می باشد
نتیجه: به غیر از عدد 2 سایر اعداد زوج، عدد اول نیستند؛ به عبارت دیگر اگر عددی زوج باشد و نیز آن عدد 2 نباشد نتیجه می گیریم که آن عدد، عدد اول نیست.
عدد زوج 32 بر 2 بخش پذیر است پس 32 عددی اول نیست و همچنین اعداد زوج 34، 36، 38، 40، 42 و … عدد اول نیستند(چون تنها عدد زوجی که عدد اول است عدد 2)
عدد 33 بر 3 بخش پذیر است پس 33 عددی اول نیست
اگر دقت کنید می بینید که هر عددی که بر 3 بخش پذیر بوده به غیر از خود عدد 3، عدد اول نیست(مثل اعدادی که بر 2 بخش پذیر هستند به جزء خود عدد 2)
اعدادی که بر 3 بخش پذیر هستند 3، 6، 9، 12، 15، 18، 21، 24، 27، 30، 33، 36، 39، 42، … که 3 عدد اول است و سایر اعداد 6، 9، 12، 15، 18، 21، 24، 27، 30، 33، 36، 39، 42، … عدد اول نیستند
عدد 35 بر 5 بخش پذیر است پس 35 عددی اول نیست
همچنین می بینیم که هر عددی که بر 5 بخش پذیر است به غیر از خود عدد 5، عدد اول نیست
اعدادی که بر 5 بخش پذیر هستند 5، 10، 15، 20، 25، 30، 35، 40، 45، 50، 55، … که 5 عدد اول است و سایر اعداد 10، 15، 20، 25، 30، 35، 40، 45، 50، 55، … عدد اول نیستند
اعدادی که بر 7 بخش پذیر هستند 7، 14 ،21، 28، 35، 42، 49، 56، 63، 70، 77، …
هر عددی که بر 7 بخش پذیر است به غیر از خود عدد 7، عدد اول نیست
اعدادی که بر 11 بخش پذیر هستند 11، 22، 33، 44، 55، 66، 77، 88، 99، 121، …
هر عددی که بر 11 بخش پذیر است به غیر از خود عدد 11، عدد اول نیست
اعدادی که بر 13 بخش پذیر هستند 13، 26، 39، 52، 65، 78، …
هر عددی که بر 13 بخش پذیر است به غیر از خود عدد 13، عدد اول نیست
این موضوع برای سایر اعداد اولی که تا حالا بدست آوردیم تکرار می شود
عدد 37 تنها بر 1 و 37 بخش پذیر است پس 37 عددی اول است
عدد 39 بر 3 بخش پذیر است پس 39 عددی اول نیست
عدد 41 تنها بر 1 و 41 بخش پذیر است پس 41 عددی اول است
اعداد اولی که تا اینجا بدست آوردیم
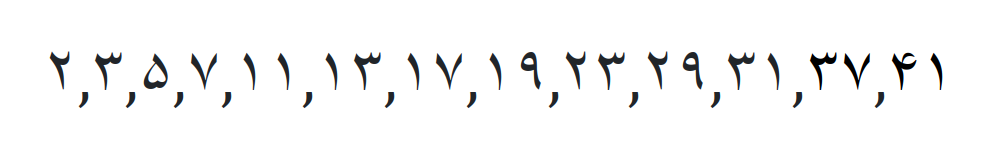
می توان با بررسی بخش پذیری اعداد بر اعداد اول 2 و ۳ و ۵ و ۷ و 11 و 13 و … عدد اول بودن یا نیودن آن عدد را مشخص کرد.
مثال:
عدد اول بودن یا نبودن اعداد 1394، 1395، 1396، 1397، 1398، 1399، 1400 را بررسی کنید.
جواب: خیلی راحت در مورد اعداد 1394، 1396، 1398، 1400 با توجه به اینکه عدد زوج هستند(بر 2 بخش پذیرند) نتیجه می گیریم که عدد اول نیستند.
عدد 1395 بر 5 بخشپذیر است(چه اعدادی بر 5 بخش پذیر هستند؟) چون حاصل تقسیم عددی صحیح مثبت بوده(عدد 279) و باقیمانده تقسیم نیز صفر است پس عدد 1395 عدد اول نیست
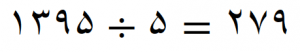
عدد 1397
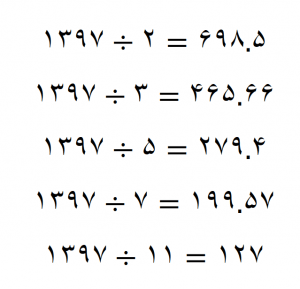
عدد 1397 بر 11 بخشپذیر است چون حاصل تقسیم عددی صحیح مثبت بوده(عدد 127) و باقیمانده تقسیم نیز صفر می شود پس عدد 1397 عدد اول نیست
توجه داشته باشید که برای بخش پذیر بودن باید حاصل تقسیم، یک عدد صحیح باشد چون حاصل تقسیم عدد 1397 بر 2، 3، 5، 7 عدد اعشاری شده پس عدد 1397 بر 2، 3، 5، 7 بخشپذیر نبود
عدد 1399
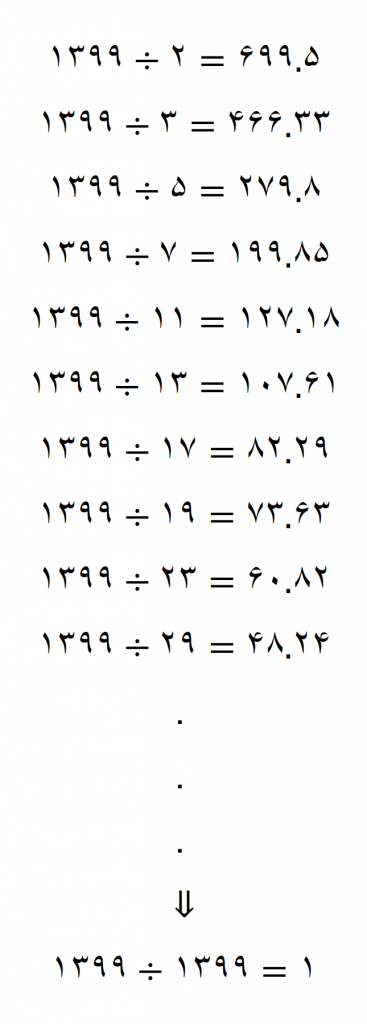
عدد 1399 تنها بر 1399 بخش پذیر است که اگر قرار باشد واقعاً تقسیم های بالا را انجام دهیم باید 222 بار عمل تقسیم را تکرار کنیم که نشان می دهد که این روش برای اعداد بزرگ روش نامناسبی است
آیا واقعاً لازم است که تمام این تقسیم ها را تا رسیدن به عدد 1399 انجام دهیم؟!
خیر؛ در حقیقت تنها کافی است که 2 تا تقسیم دیگر را برای رسیدن به نتیجه که اول بودن این عدد است انجام دهیم(چرا؟!)
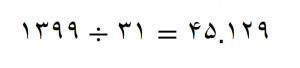
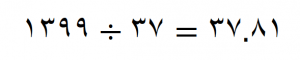
مربع عدد 41 برابر است با ۱۶۸۱ و این همان دلیلی است که نیاز نیست دیگر به این تقسیم ادامه دهیم یعنی وقتی مربع عدد اول، از عدد مورد نظر بزرگتر شود ما دیگر تقسیم بر عددهای اول را ادامه نمی دهیم
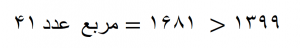
عدد 1399 به جز خودش به هیچ یک از این اعداد اول بخشپذیر نیست پس عدد 1399 عدد اول است
تشخیص عدد اول بودن یا اول نبودن یک عدد
برای تشخیص این که یک عدد، عدد اول است یا نه، کافی است آن عدد را بر اعداد اول کوچکتر از جذرش تقسیم کنیم که اگر بر هیچ یک از آن ها بخش پذیر نبود، عدد اول است و در غیر این صورت عدد اول نیست.
مثال: عدد 1399 را دوباره در نظر می گیریم
جواب: جذر 1399 تقریباً 37.40 (مقدار دقیق جذر اهمیتی ندارد) یعنی ما باید بخش پذیری عدد 1399 را بر اعداد اولی که از 37.40 کوچکتر هستند مورد بررسی قرار دهیم بعنی اعداد زیر
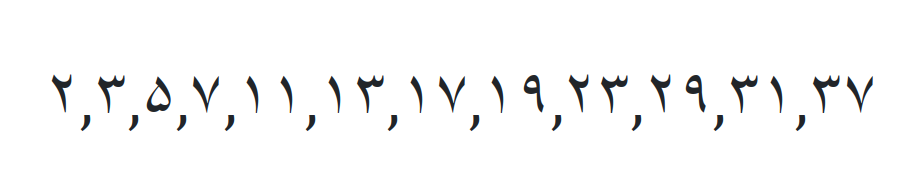
عدد اول بعد از 37، عدد 41 است پس جذر 1399 بین اعداد اول 37 و 41 قرار دارد
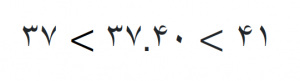
البته وقتی از جذر استفاده می کنیم نیازی نیست که ما عدد اول بعد از 37 را بدانیم تنها باید اعداد اولی که کوچکتر از 37.40 هستند را برای بخش پذیری بررسی کنیم ولی برای در نظر گرفتن مربع عدد اول لازم است که ما عدد اول بعد از 37 را بدانیم
می توان به جای جذر، مربع عدد را در نظر گرفت
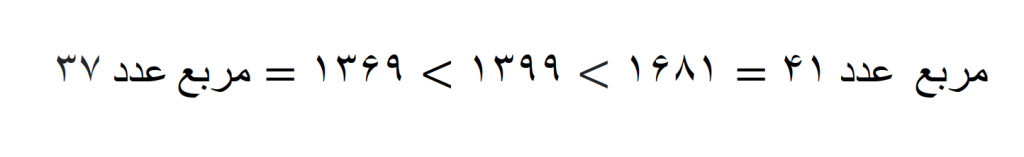
که همان طور که قبلاً بررسی کردیم عدد 1399 بر هیچکدام از اعداد اول
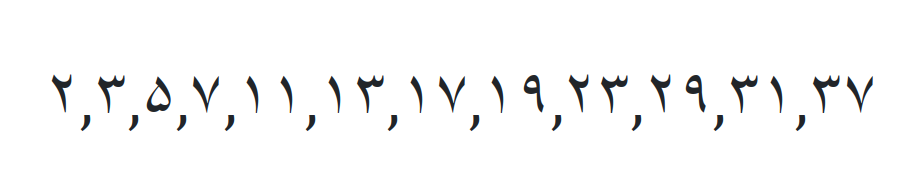
بخشپذیر نیست بنابراین 1399 عدد اول است.
نکته: به هر عدد طبیعی مخالف 1 که عدد اول نباشد، عدد مرکب می گویند.
نکته: عدد 1 نه عدد اول است و نه عدد مرکب.
نکته: صفر بر همه اعداد صحیح بخشپذیر است.
نکته: هر عدد صحیحی بر 1 بخشپذیر است.
اعداد اول از مجموعه نامتناهی اعداد طبیعی هستند که در نتیجه خود اعداد اول نیز یک مجموعه نامتناهی را تشکیل می دهند.
یک روش برای یافتن اعداد اول، روش غربال است که برای تعیین اعداد اول در محدوده ای از اعداد(یک بازه مشخص) استفاده می شود.
فهرست ۱۰۰۰ عدد اول
| ۲ | ۳ | ۵ | ۷ | ۱۱ | ۱۳ | ۱۷ | ۱۹ | ۲۳ | ۲۹ | ۳۱ | ۳۷ | ۴۱ | ۴۳ | ۴۷ | ۵۳ | ۵۹ | ۶۱ | ۶۷ | ۷۱ |
| ۷۳ | ۷۹ | ۸۳ | ۸۹ | ۹۷ | ۱۰۱ | ۱۰۳ | ۱۰۷ | ۱۰۹ | ۱۱۳ | ۱۲۷ | ۱۳۱ | ۱۳۷ | ۱۳۹ | ۱۴۹ | ۱۵۱ | ۱۵۷ | ۱۶۳ | ۱۶۷ | ۱۷۳ |
| ۱۷۹ | ۱۸۱ | ۱۹۱ | ۱۹۳ | ۱۹۷ | ۱۹۹ | ۲۱۱ | ۲۲۳ | ۲۲۷ | ۲۲۹ | ۲۳۳ | ۲۳۹ | ۲۴۱ | ۲۵۱ | ۲۵۷ | ۲۶۳ | ۲۶۹ | ۲۷۱ | ۲۷۷ | ۲۸۱ |
| ۲۸۳ | ۲۹۳ | ۳۰۷ | ۳۱۱ | ۳۱۳ | ۳۱۷ | ۳۳۱ | ۳۳۷ | ۳۴۷ | ۳۴۹ | ۳۵۳ | ۳۵۹ | ۳۶۷ | ۳۷۳ | ۳۷۹ | ۳۸۳ | ۳۸۹ | ۳۹۷ | ۴۰۱ | ۴۰۹ |
| ۴۱۹ | ۴۲۱ | ۴۳۱ | ۴۳۳ | ۴۳۹ | ۴۴۳ | ۴۴۹ | ۴۵۷ | ۴۶۱ | ۴۶۳ | ۴۶۷ | ۴۷۹ | ۴۸۷ | ۴۹۱ | ۴۹۹ | ۵۰۳ | ۵۰۹ | ۵۲۱ | ۵۲۳ | ۵۴۱ |
| ۵۴۷ | ۵۵۷ | ۵۶۳ | ۵۶۹ | ۵۷۱ | ۵۷۷ | ۵۸۷ | ۵۹۳ | ۵۹۹ | ۶۰۱ | ۶۰۷ | ۶۱۳ | ۶۱۷ | ۶۱۹ | ۶۳۱ | ۶۴۱ | ۶۴۳ | ۶۴۷ | ۶۵۳ | ۶۵۹ |
| ۶۶۱ | ۶۷۳ | ۶۷۷ | ۶۸۳ | ۶۹۱ | ۷۰۱ | ۷۰۹ | ۷۱۹ | ۷۲۷ | ۷۳۳ | ۷۳۹ | ۷۴۳ | ۷۵۱ | ۷۵۷ | ۷۶۱ | ۷۶۹ | ۷۷۳ | ۷۸۷ | ۷۹۷ | ۸۰۹ |
| ۸۱۱ | ۸۲۱ | ۸۲۳ | ۸۲۷ | ۸۲۹ | ۸۳۹ | ۸۵۳ | ۸۵۷ | ۸۵۹ | ۸۶۳ | ۸۷۷ | ۸۸۱ | ۸۸۳ | ۸۸۷ | ۹۰۷ | ۹۱۱ | ۹۱۹ | ۹۲۹ | ۹۳۷ | ۹۴۱ |
| ۹۴۷ | ۹۵۳ | ۹۶۷ | ۹۷۱ | ۹۷۷ | ۹۸۳ | ۹۹۱ | ۹۹۷ | ۱۰۰۹ | ۱۰۱۳ | ۱۰۱۹ | ۱۰۲۱ | ۱۰۳۱ | ۱۰۳۳ | ۱۰۳۹ | ۱۰۴۹ | ۱۰۵۱ | ۱۰۶۱ | ۱۰۶۳ | ۱۰۶۹ |
| ۱۰۸۷ | ۱۰۹۱ | ۱۰۹۳ | ۱۰۹۷ | ۱۱۰۳ | ۱۱۰۹ | ۱۱۱۷ | ۱۱۲۳ | ۱۱۲۹ | ۱۱۵۱ | ۱۱۵۳ | ۱۱۶۳ | ۱۱۷۱ | ۱۱۸۱ | ۱۱۸۷ | ۱۱۹۳ | ۱۲۰۱ | ۱۲۱۳ | ۱۲۱۷ | ۱۲۲۳ |
| ۱۲۲۹ | ۱۲۳۱ | ۱۲۳۷ | ۱۲۴۹ | ۱۲۵۹ | ۱۲۷۷ | ۱۲۷۹ | ۱۲۸۳ | ۱۲۸۹ | ۱۲۹۱ | ۱۲۹۷ | ۱۳۰۱ | ۱۳۰۳ | ۱۳۰۷ | ۱۳۱۹ | ۱۳۲۱ | ۱۳۲۷ | ۱۳۶۱ | ۱۳۶۷ | ۱۳۷۳ |
| ۱۳۸۱ | ۱۳۹۹ | ۱۴۰۹ | ۱۴۲۳ | ۱۴۲۷ | ۱۴۲۹ | ۱۴۳۳ | ۱۴۳۹ | ۱۴۴۷ | ۱۴۵۱ | ۱۴۵۳ | ۱۴۵۹ | ۱۴۷۱ | ۱۴۸۱ | ۱۴۸۳ | ۱۴۸۷ | ۱۴۸۹ | ۱۴۹۳ | ۱۴۹۹ | ۱۵۱۱ |
| ۱۵۲۳ | ۱۵۳۱ | ۱۵۴۳ | ۱۵۴۹ | ۱۵۵۳ | ۱۵۵۹ | ۱۵۶۷ | ۱۵۷۱ | ۱۵۷۹ | ۱۵۸۳ | ۱۵۹۷ | ۱۶۰۱ | ۱۶۰۷ | ۱۶۰۹ | ۱۶۱۳ | ۱۶۱۹ | ۱۶۲۱ | ۱۶۲۷ | ۱۶۳۷ | ۱۶۵۷ |
| ۱۶۶۳ | ۱۶۶۷ | ۱۶۶۹ | ۱۶۹۳ | ۱۶۹۷ | ۱۶۹۹ | ۱۷۰۹ | ۱۷۲۱ | ۱۷۲۳ | ۱۷۳۳ | ۱۷۴۱ | ۱۷۴۷ | ۱۷۵۳ | ۱۷۵۹ | ۱۷۷۷ | ۱۷۸۳ | ۱۷۸۷ | ۱۷۸۹ | ۱۸۰۱ | ۱۸۱۱ |
| ۱۸۲۳ | ۱۸۳۱ | ۱۸۴۷ | ۱۸۶۱ | ۱۸۶۷ | ۱۸۷۱ | ۱۸۷۳ | ۱۸۷۷ | ۱۸۷۹ | ۱۸۸۹ | ۱۹۰۱ | ۱۹۰۷ | ۱۹۱۳ | ۱۹۳۱ | ۱۹۳۳ | ۱۹۴۹ | ۱۹۵۱ | ۱۹۷۳ | ۱۹۷۹ | ۱۹۸۷ |
| ۱۹۹۳ | ۱۹۹۷ | ۱۹۹۹ | ۲۰۰۳ | ۲۰۱۱ | ۲۰۱۷ | ۲۰۲۷ | ۲۰۲۹ | ۲۰۳۹ | ۲۰۵۳ | ۲۰۶۳ | ۲۰۶۹ | ۲۰۸۱ | ۲۰۸۳ | ۲۰۸۷ | ۲۰۸۹ | ۲۰۹۹ | ۲۱۱۱ | ۲۱۱۳ | ۲۱۲۹ |
| ۲۱۳۱ | ۲۱۳۷ | ۲۱۴۱ | ۲۱۴۳ | ۲۱۵۳ | ۲۱۶۱ | ۲۱۷۹ | ۲۲۰۳ | ۲۲۰۷ | ۲۲۱۳ | ۲۲۲۱ | ۲۲۳۷ | ۲۲۳۹ | ۲۲۴۳ | ۲۲۵۱ | ۲۲۶۷ | ۲۲۶۹ | ۲۲۷۳ | ۲۲۸۱ | ۲۲۸۷ |
| ۲۲۹۳ | ۲۲۹۷ | ۲۳۰۹ | ۲۳۱۱ | ۲۳۳۳ | ۲۳۳۹ | ۲۳۴۱ | ۲۳۴۷ | ۲۳۵۱ | ۲۳۵۷ | ۲۳۷۱ | ۲۳۷۷ | ۲۳۸۱ | ۲۳۸۳ | ۲۳۸۹ | ۲۳۹۳ | ۲۳۹۹ | ۲۴۱۱ | ۲۴۱۷ | ۲۴۲۳ |
| ۲۴۳۷ | ۲۴۴۱ | ۲۴۴۷ | ۲۴۵۹ | ۲۴۶۷ | ۲۴۷۳ | ۲۴۷۷ | ۲۵۰۳ | ۲۵۲۱ | ۲۵۳۱ | ۲۵۳۹ | ۲۵۴۳ | ۲۵۴۹ | ۲۵۵۱ | ۲۵۵۷ | ۲۵۷۹ | ۲۵۹۱ | ۲۵۹۳ | ۲۶۰۹ | ۲۶۱۷ |
| ۲۶۲۱ | ۲۶۳۳ | ۲۶۴۷ | ۲۶۵۷ | ۲۶۵۹ | ۲۶۶۳ | ۲۶۷۱ | ۲۶۷۷ | ۲۶۸۳ | ۲۶۸۷ | ۲۶۸۹ | ۲۶۹۳ | ۲۶۹۹ | ۲۷۰۷ | ۲۷۱۱ | ۲۷۱۳ | ۲۷۱۹ | ۲۷۲۹ | ۲۷۳۱ | ۲۷۴۱ |
| ۲۷۴۹ | ۲۷۵۳ | ۲۷۶۷ | ۲۷۷۷ | ۲۷۸۹ | ۲۷۹۱ | ۲۷۹۷ | ۲۸۰۱ | ۲۸۰۳ | ۲۸۱۹ | ۲۸۳۳ | ۲۸۳۷ | ۲۸۴۳ | ۲۸۵۱ | ۲۸۵۷ | ۲۸۶۱ | ۲۸۷۹ | ۲۸۸۷ | ۲۸۹۷ | ۲۹۰۳ |
| ۲۹۰۹ | ۲۹۱۷ | ۲۹۲۷ | ۲۹۳۹ | ۲۹۵۳ | ۲۹۵۷ | ۲۹۶۳ | ۲۹۶۹ | ۲۹۷۱ | ۲۹۹۹ | ۳۰۰۱ | ۳۰۱۱ | ۳۰۱۹ | ۳۰۲۳ | ۳۰۳۷ | ۳۰۴۱ | ۳۰۴۹ | ۳۰۶۱ | ۳۰۶۷ | ۳۰۷۹ |
| ۳۰۸۳ | ۳۰۸۹ | ۳۱۰۹ | ۳۱۱۹ | ۳۱۲۱ | ۳۱۳۷ | ۳۱۶۳ | ۳۱۶۷ | ۳۱۶۹ | ۳۱۸۱ | ۳۱۸۷ | ۳۱۹۱ | ۳۲۰۳ | ۳۲۰۹ | ۳۲۱۷ | ۳۲۲۱ | ۳۲۲۹ | ۳۲۵۱ | ۳۲۵۳ | ۳۲۵۷ |
| ۳۲۵۹ | ۳۲۷۱ | ۳۲۹۹ | ۳۳۰۱ | ۳۳۰۷ | ۳۳۱۳ | ۳۳۱۹ | ۳۳۲۳ | ۳۳۲۹ | ۳۳۳۱ | ۳۳۴۳ | ۳۳۴۷ | ۳۳۵۹ | ۳۳۶۱ | ۳۳۷۱ | ۳۳۷۳ | ۳۳۸۹ | ۳۳۹۱ | ۳۴۰۷ | ۳۴۱۳ |
| ۳۴۳۳ | ۳۴۴۹ | ۳۴۵۷ | ۳۴۶۱ | ۳۴۶۳ | ۳۴۶۷ | ۳۴۶۹ | ۳۴۹۱ | ۳۴۹۹ | ۳۵۱۱ | ۳۵۱۷ | ۳۵۲۷ | ۳۵۲۹ | ۳۵۳۳ | ۳۵۳۹ | ۳۵۴۱ | ۳۵۴۷ | ۳۵۵۷ | ۳۵۵۹ | ۳۵۷۱ |
| ۳۵۸۱ | ۳۵۸۳ | ۳۵۹۳ | ۳۶۰۷ | ۳۶۱۳ | ۳۶۱۷ | ۳۶۲۳ | ۳۶۳۱ | ۳۶۳۷ | ۳۶۴۳ | ۳۶۵۹ | ۳۶۷۱ | ۳۶۷۳ | ۳۶۷۷ | ۳۶۹۱ | ۳۶۹۷ | ۳۷۰۱ | ۳۷۰۹ | ۳۷۱۹ | ۳۷۲۷ |
| ۳۷۳۳ | ۳۷۳۹ | ۳۷۶۱ | ۳۷۶۷ | ۳۷۶۹ | ۳۷۷۹ | ۳۷۹۳ | ۳۷۹۷ | ۳۸۰۳ | ۳۸۲۱ | ۳۸۲۳ | ۳۸۳۳ | ۳۸۴۷ | ۳۸۵۱ | ۳۸۵۳ | ۳۸۶۳ | ۳۸۷۷ | ۳۸۸۱ | ۳۸۸۹ | ۳۹۰۷ |
| ۳۹۱۱ | ۳۹۱۷ | ۳۹۱۹ | ۳۹۲۳ | ۳۹۲۹ | ۳۹۳۱ | ۳۹۴۳ | ۳۹۴۷ | ۳۹۶۷ | ۳۹۸۹ | ۴۰۰۱ | ۴۰۰۳ | ۴۰۰۷ | ۴۰۱۳ | ۴۰۱۹ | ۴۰۲۱ | ۴۰۲۷ | ۴۰۴۹ | ۴۰۵۱ | ۴۰۵۷ |
| ۴۰۷۳ | ۴۰۷۹ | ۴۰۹۱ | ۴۰۹۳ | ۴۰۹۹ | ۴۱۱۱ | ۴۱۲۷ | ۴۱۲۹ | ۴۱۳۳ | ۴۱۳۹ | ۴۱۵۳ | ۴۱۵۷ | ۴۱۵۹ | ۴۱۷۷ | ۴۲۰۱ | ۴۲۱۱ | ۴۲۱۷ | ۴۲۱۹ | ۴۲۲۹ | ۴۲۳۱ |
| ۴۲۴۱ | ۴۲۴۳ | ۴۲۵۳ | ۴۲۵۹ | ۴۲۶۱ | ۴۲۷۱ | ۴۲۷۳ | ۴۲۸۳ | ۴۲۸۹ | ۴۲۹۷ | ۴۳۲۷ | ۴۳۳۷ | ۴۳۳۹ | ۴۳۴۹ | ۴۳۵۷ | ۴۳۶۳ | ۴۳۷۳ | ۴۳۹۱ | ۴۳۹۷ | ۴۴۰۹ |
| ۴۴۲۱ | ۴۴۲۳ | ۴۴۴۱ | ۴۴۴۷ | ۴۴۵۱ | ۴۴۵۷ | ۴۴۶۳ | ۴۴۸۱ | ۴۴۸۳ | ۴۴۹۳ | ۴۵۰۷ | ۴۵۱۳ | ۴۵۱۷ | ۴۵۱۹ | ۴۵۲۳ | ۴۵۴۷ | ۴۵۴۹ | ۴۵۶۱ | ۴۵۶۷ | ۴۵۸۳ |
| ۴۵۹۱ | ۴۵۹۷ | ۴۶۰۳ | ۴۶۲۱ | ۴۶۳۷ | ۴۶۳۹ | ۴۶۴۳ | ۴۶۴۹ | ۴۶۵۱ | ۴۶۵۷ | ۴۶۶۳ | ۴۶۷۳ | ۴۶۷۹ | ۴۶۹۱ | ۴۷۰۳ | ۴۷۲۱ | ۴۷۲۳ | ۴۷۲۹ | ۴۷۳۳ | ۴۷۵۱ |
| ۴۷۵۹ | ۴۷۸۳ | ۴۷۸۷ | ۴۷۸۹ | ۴۷۹۳ | ۴۷۹۹ | ۴۸۰۱ | ۴۸۱۳ | ۴۸۱۷ | ۴۸۳۱ | ۴۸۶۱ | ۴۸۷۱ | ۴۸۷۷ | ۴۸۸۹ | ۴۹۰۳ | ۴۹۰۹ | ۴۹۱۹ | ۴۹۳۱ | ۴۹۳۳ | ۴۹۳۷ |
| ۴۹۴۳ | ۴۹۵۱ | ۴۹۵۷ | ۴۹۶۷ | ۴۹۶۹ | ۴۹۷۳ | ۴۹۸۷ | ۴۹۹۳ | ۴۹۹۹ | ۵۰۰۳ | ۵۰۰۹ | ۵۰۱۱ | ۵۰۲۱ | ۵۰۲۳ | ۵۰۳۹ | ۵۰۵۱ | ۵۰۵۹ | ۵۰۷۷ | ۵۰۸۱ | ۵۰۸۷ |
| ۵۰۹۹ | ۵۱۰۱ | ۵۱۰۷ | ۵۱۱۳ | ۵۱۱۹ | ۵۱۴۷ | ۵۱۵۳ | ۵۱۶۷ | ۵۱۷۱ | ۵۱۷۹ | ۵۱۸۹ | ۵۱۹۷ | ۵۲۰۹ | ۵۲۲۷ | ۵۲۳۱ | ۵۲۳۳ | ۵۲۳۷ | ۵۲۶۱ | ۵۲۷۳ | ۵۲۷۹ |
| ۵۲۸۱ | ۵۲۹۷ | ۵۳۰۳ | ۵۳۰۹ | ۵۳۲۳ | ۵۳۳۳ | ۵۳۴۷ | ۵۳۵۱ | ۵۳۸۱ | ۵۳۸۷ | ۵۳۹۳ | ۵۳۹۹ | ۵۴۰۷ | ۵۴۱۳ | ۵۴۱۷ | ۵۴۱۹ | ۵۴۳۱ | ۵۴۳۷ | ۵۴۴۱ | ۵۴۴۳ |
| ۵۴۴۹ | ۵۴۷۱ | ۵۴۷۷ | ۵۴۷۹ | ۵۴۸۳ | ۵۵۰۱ | ۵۵۰۳ | ۵۵۰۷ | ۵۵۱۹ | ۵۵۲۱ | ۵۵۲۷ | ۵۵۳۱ | ۵۵۵۷ | ۵۵۶۳ | ۵۵۶۹ | ۵۵۷۳ | ۵۵۸۱ | ۵۵۹۱ | ۵۶۲۳ | ۵۶۳۹ |
| ۵۶۴۱ | ۵۶۴۷ | ۵۶۵۱ | ۵۶۵۳ | ۵۶۵۷ | ۵۶۵۹ | ۵۶۶۹ | ۵۶۸۳ | ۵۶۸۹ | ۵۶۹۳ | ۵۷۰۱ | ۵۷۱۱ | ۵۷۱۷ | ۵۷۳۷ | ۵۷۴۱ | ۵۷۴۳ | ۵۷۴۹ | ۵۷۷۹ | ۵۷۸۳ | ۵۷۹۱ |
| ۵۸۰۱ | ۵۸۰۷ | ۵۸۱۳ | ۵۸۲۱ | ۵۸۲۷ | ۵۸۳۹ | ۵۸۴۳ | ۵۸۴۹ | ۵۸۵۱ | ۵۸۵۷ | ۵۸۶۱ | ۵۸۶۷ | ۵۸۶۹ | ۵۸۷۹ | ۵۸۸۱ | ۵۸۹۷ | ۵۹۰۳ | ۵۹۲۳ | ۵۹۲۷ | ۵۹۳۹ |
| ۵۹۵۳ | ۵۹۸۱ | ۵۹۸۷ | ۶۰۰۷ | ۶۰۱۱ | ۶۰۲۹ | ۶۰۳۷ | ۶۰۴۳ | ۶۰۴۷ | ۶۰۵۳ | ۶۰۶۷ | ۶۰۷۳ | ۶۰۷۹ | ۶۰۸۹ | ۶۰۹۱ | ۶۱۰۱ | ۶۱۱۳ | ۶۱۲۱ | ۶۱۳۱ | ۶۱۳۳ |
| ۶۱۴۳ | ۶۱۵۱ | ۶۱۶۳ | ۶۱۷۳ | ۶۱۹۷ | ۶۱۹۹ | ۶۲۰۳ | ۶۲۱۱ | ۶۲۱۷ | ۶۲۲۱ | ۶۲۲۹ | ۶۲۴۷ | ۶۲۵۷ | ۶۲۶۳ | ۶۲۶۹ | ۶۲۷۱ | ۶۲۷۷ | ۶۲۸۷ | ۶۲۹۹ | ۶۳۰۱ |
| ۶۳۱۱ | ۶۳۱۷ | ۶۳۲۳ | ۶۳۲۹ | ۶۳۳۷ | ۶۳۴۳ | ۶۳۵۳ | ۶۳۵۹ | ۶۳۶۱ | ۶۳۶۷ | ۶۳۷۳ | ۶۳۷۹ | ۶۳۸۹ | ۶۳۹۷ | ۶۴۲۱ | ۶۴۲۷ | ۶۴۴۹ | ۶۴۵۱ | ۶۴۶۹ | ۶۴۷۳ |
| ۶۴۸۱ | ۶۴۹۱ | ۶۵۲۱ | ۶۵۲۹ | ۶۵۴۷ | ۶۵۵۱ | ۶۵۵۳ | ۶۵۶۳ | ۶۵۶۹ | ۶۵۷۱ | ۶۵۷۷ | ۶۵۸۱ | ۶۵۹۹ | ۶۶۰۷ | ۶۶۱۹ | ۶۶۳۷ | ۶۶۵۳ | ۶۶۵۹ | ۶۶۶۱ | ۶۶۷۳ |
| ۶۶۷۹ | ۶۶۸۹ | ۶۶۹۱ | ۶۷۰۱ | ۶۷۰۳ | ۶۷۰۹ | ۶۷۱۹ | ۶۷۳۳ | ۶۷۳۷ | ۶۷۶۱ | ۶۷۶۳ | ۶۷۷۹ | ۶۷۸۱ | ۶۷۹۱ | ۶۷۹۳ | ۶۸۰۳ | ۶۸۲۳ | ۶۸۲۷ | ۶۸۲۹ | ۶۸۳۳ |
| ۶۸۴۱ | ۶۸۵۷ | ۶۸۶۳ | ۶۸۶۹ | ۶۸۷۱ | ۶۸۸۳ | ۶۸۹۹ | ۶۹۰۷ | ۶۹۱۱ | ۶۹۱۷ | ۶۹۴۷ | ۶۹۴۹ | ۶۹۵۹ | ۶۹۶۱ | ۶۹۶۷ | ۶۹۷۱ | ۶۹۷۷ | ۶۹۸۳ | ۶۹۹۱ | ۶۹۹۷ |
| ۷۰۰۱ | ۷۰۱۳ | ۷۰۱۹ | ۷۰۲۷ | ۷۰۳۹ | ۷۰۴۳ | ۷۰۵۷ | ۷۰۶۹ | ۷۰۷۹ | ۷۱۰۳ | ۷۱۰۹ | ۷۱۲۱ | ۷۱۲۷ | ۷۱۲۹ | ۷۱۵۱ | ۷۱۵۹ | ۷۱۷۷ | ۷۱۸۷ | ۷۱۹۳ | ۷۲۰۷ |
| ۷۲۱۱ | ۷۲۱۳ | ۷۲۱۹ | ۷۲۲۹ | ۷۲۳۷ | ۷۲۴۳ | ۷۲۴۷ | ۷۲۵۳ | ۷۲۸۳ | ۷۲۹۷ | ۷۳۰۷ | ۷۳۰۹ | ۷۳۲۱ | ۷۳۳۱ | ۷۳۳۳ | ۷۳۴۹ | ۷۳۵۱ | ۷۳۶۹ | ۷۳۹۳ | ۷۴۱۱ |
| ۷۴۱۷ | ۷۴۳۳ | ۷۴۵۱ | ۷۴۵۷ | ۷۴۵۹ | ۷۴۷۷ | ۷۴۸۱ | ۷۴۸۷ | ۷۴۸۹ | ۷۴۹۹ | ۷۵۰۷ | ۷۵۱۷ | ۷۵۲۳ | ۷۵۲۹ | ۷۵۳۷ | ۷۵۴۱ | ۷۵۴۷ | ۷۵۴۹ | ۷۵۵۹ | ۷۵۶۱ |
| ۷۵۷۳ | ۷۵۷۷ | ۷۵۸۳ | ۷۵۸۹ | ۷۵۹۱ | ۷۶۰۳ | ۷۶۰۷ | ۷۶۲۱ | ۷۶۳۹ | ۷۶۴۳ | ۷۶۴۹ | ۷۶۶۹ | ۷۶۷۳ | ۷۶۸۱ | ۷۶۸۷ | ۷۶۹۱ | ۷۶۹۹ | ۷۷۰۳ | ۷۷۱۷ | ۷۷۲۳ |
| ۷۷۲۷ | ۷۷۴۱ | ۷۷۵۳ | ۷۷۵۷ | ۷۷۵۹ | ۷۷۸۹ | ۷۷۹۳ | ۷۸۱۷ | ۷۸۲۳ | ۷۸۲۹ | ۷۸۴۱ | ۷۸۵۳ | ۷۸۶۷ | ۷۸۷۳ | ۷۸۷۷ | ۷۸۷۹ | ۷۸۸۳ | ۷۹۰۱ | ۷۹۰۷ | ۷۹۱۹ |
دانلود لیست 100008 عدد اول نخست
فایل فشرده به فرمت zip است(داخل این فایل فشرده 2 فایل است، یکی با فرمت متنی txt و دیگری با فرمت html)
لینک کوتاه این مطلب: https://tadris.dabidi.ir/prime
تعریف و تشخیص اعداد اول به همراه لیست

